学习RL(四)

Learning就是通过迭代的方法找到更接近真实值的手段。

蒙特卡洛方法

当研究的问题动态模型未知的时候，怎么做策略估计？怎么做策略的改进？

在实际应用中，经常遇到模型未知的情况，无法像上一章节讲的，通过Bellman公式计算状态价值是根据模型（状态传递概率）得到的，但是实际应用中经常遇到没有这样的概率可以依赖。

思路就是既然MDP利用环境状态传递概率(State Transition Probability)来加权计算期望，在不知道这个概率的情况下，能否利用多次采集某状态出现的时候，环境给出的奖励Reward来平均计算，作为状态价值。

解法就是通过实验，多次执行episode，在每次的循环中，记录特定状态出现的次数以及循环结束之后所获得的奖励，最后依据大数定律，对积累起来的奖励求平均值，就当作该状态的价值。如果我们事先知道所有的可能状态（在该特定的policy下面，应该可以确定出来），那么就维护一个数组，存储每一种状态的上面的信息，最后所有状态的价值都计算出来就意味着策略评估完成了。 但是问题来了：如果一个episode持续很长时间，或者就无法结束，那么，蒙特卡洛方法这种依赖episode结束才可以获得状态价值的方法就无法应用，需要找到替代的方法来近似。 TD-learning就解决了这个问题。基于TD-Learning就衍生出一系列的方法解决这类问题。

MC Policy Evaluation and Control

1. 需要循环多次episode, 每次episode开始之后，第一次每一次遇到感兴趣的，记录，并且把Return加进来：
2. 完成当前的episode后，计算 ->类似于累加Reward的过程
3. 然后遍历，更新策略：

书中提到的Monte Carlo ES，是指每一个episode起始的状态选择是随机的，不能固定，避免有些状态永远无法被访问到。下图是书中的算法流程。

这部分也叫做MC Policy Improvement。 从给定的开始，代表策略估计（Policy Estimation），得到动作价值函数，采用贪心算法（greedy）找到使得最大的action:

参看4.6 广义策略迭代(Generalized Policy Iteration)

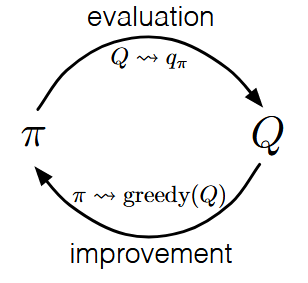
On-Policy and Off-Policy

TD Learning

MC方法需要走完一个完整episode才可以计算，但是TD方法不需要，每次采取完行动之后，立刻马上就可以更新状态价值。 该方法只是在特定的策略下，不断迭代找到状态价值。所以，是一种Learning的方法。后面，Sarsa是加入了策略改进的，是GPI的一种。

Sarsa - State Action Reward State Action

Sarsa是on-policy TD control。 很自然地，通过上面的TD Learning，一边学习，一边采用改进策略。具体过程如下： 重点看代表采取行动之后环境给出的状态为的行动价值，后面的Expected Sarsa改进为求所有可能造成的全部的加权平均，希望能够更加快速贴近真实的行动价值。

Q-Learning - off-policy TD control

Q-Learning是一种off-policy的学习方法，是因为：在每次迭代的过程中，它只是学习到Optimal Policy，但是并没有在学习过程中，根据更新了的Policy去沿用新的策略采取行动。 [Question::每次迭代之后，难道不会收敛到同一个数值吗？] [Answer::在不同的状态下，最佳的行动导致的行动价值是不一样的。]所以从这个角度理解，就会发现，Q-Learning每次更新的就是朝向Optimal Policy前进的，或者从控制的角度来看，被控对象看作是环境，如果被控对象从任何状态，采取某一种行动就可以获得最多的Reward，那么，这样的系统下，可能会收敛到同一个数值。但是，实际上，在不同状态下，如果采取相同的动作，会发现，有些动作会导致Reward很低，也就是不合理。所以，不同的状态，需要采取不同的行动，在每次行动中，得到对应的Reward，随着时间的推移，这些Reward积累起来的“求和”就逐渐“逼近了”状态价值的真实值。 Q-Learning把学习和策略优化分开，每次采取的行动不一定是根据上次学习到的最佳行动价值，就是在比较随机地选择行动的过程中，将“可能不是最好的行动”所带来的最好的价值加入到TD-Learning的行动价值更新中，以期望更快地调整行动价值，接近最优行动价值。这种做法的好处就是：做更多的探索动作，保证访问到更多的对，从而更接近真实的数值，而避免陷入局部的最优，出不来。

Expected Sarsa

行动价值的更新算法如下：

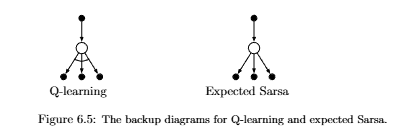Expected Sarsa在更新的时候，考虑了所有的action，而不是单个的action的行动价值。 缺点是需要计算期望，在性能方面差。

Consider the learning algorithm that is just like Q-learning except that instead of the maximum over next state–action pairs it uses the expected value, taking into account how likely each action is under the current policy. Given the next state , this algorithm moves deterministically in the same direction as Sarsa moves in expectation, and accordingly it is called Expected Sarsa.

Deep Q-Network

在实际应用中，遇到的问题经常是：的取值非常广泛，每次迭代很难做到遍历每一个动作价值。 所以，能不能有一种方法，可以找到一个函数，输入为（后面会更新成），输出就是价值。很多研究都是提出一个Linear Function Approximator去解决的估计问题，该论文提出利用ANN，非线性神经网络近似函数：neural network function approximator。 论文中提到：当尝试使用非线性的函数去逼近的时候，经常会遇到函数不稳定或者是发散的问题，具体的原因如下： 1. agent观察到的序列前后是有关联的，所以在某一段时间内的迭代过程，数据的相似性较大，会“引导”策略向不正确的（和整个数据代表的分布）方向前进，最后验证的时候，会发现在某些场景下agent的输出很优秀，但是其他的场景下表现较差。 2. 对Q做微小的调整，可能会造成剧烈的变动，从而造成之后采集到的数据分布发生剧烈变动，也造成了待估计的和引入的目标行动价值函数（target action-value function）之间发生剧烈变动。

解决的思路是： 1. 利用生物体的回忆过往experience replay，将数据的前后关联打散，并且在输入到学习网络之前，对数据进行平滑处理。 2. 对的估计，整体还是使用迭代的方法，不过这一项中的不会每次迭代都更新，而是受到一个参数（多少次迭代）控制何时去更新。在论文中，作者称这一项为target action-value function。 如果将上面的这些输入存储起来，构建一个库(agent's memory)。 每次迭代，都会计算一个下面的损失函数会发生变化，通过stochastic gradient decsent方法，可以找到，从而更新，作为下一次计算的参数。

• 下面的算法中，就是target action-value function，它的大小由和决定。
• 的更新方向是
• 经过次迭代，更新 ## 参考 David Silver's video Lil'Log Sutton's Book