学习RL(三)

第四章节 动态规划

4.4 价值迭代

上一篇笔记当中的JCR的例子的实现过程，是将策略评估和策略改进分开进行的，具体地讲，就是在策略评估阶段，需要针对每个状态，在给定的策略下，做Bellman计算得到新状态价值，然后拿着这个给到策略改进阶段，在这个阶段当中，针对每个状态，遍历所有的可能行动，计算得到一组行动价值（action-value），然后选择最大的行动价值，替换掉当前状态对应的行动。完成上述的一个循环过程，是很耗时间的。

价值迭代解决的是如何提高上述两个阶段的效率，以达到一个更快找到最优策略的目的。

思路就是在策略评估阶段，先不要着急根据当前的策略去更新状态价值，而是遍历一下所有的行动，找到在当前状态下使得行动价值最大化的那个行动，直接替换该状态的行动，根据这个行动做Bellman的计算更新状态价值，最终循环这个过程直到状态价值变化很小达到收敛。

价值迭代算法流程

赌徒（Gambler）问题

具体的问题描述就不在这里赘述了。下面记录一下实现代码过程中遇到的问题。

代码实现过程中遇到的理解问题

1. 价值迭代最核心的点是在某一个状态下，直接遍历所有的actions, 计算出一组, 在这组数当中找到最大的那个，对应的变为，并且需要随时将更大的替换掉当前的状态价值函数。这里需要注意，可能在尚未找到最优动作之前，已经做了若干次的更新。
2. updateStateValue函数需要根据Bellman方程来更新状态价值，我最开始的实现错误地将Reward设置为1，这样造成的结果是计算出很大的。
3. 最后计算出来的策略结果和书中有出入，作者提到了最优解是不唯一的，我仔细看了最后一次迭代的中间结果，发现采取两个不同的行动，对应计算出来的状态价值差距特别小，在小数点后10位了，所以这种情况下，其实选择任意一个都是最优的。
   python 代码

   import matplotlib.pyplot as plt
   import numpy as np
   import math
   from mpl_toolkits.mplot3d import Axes3D 
   import matplotlib.animation as animation
   import matplotlib.colors as colors
   import matplotlib.cm as cm
   from matplotlib.ticker import MultipleLocator
   
   CONST_GOAL = 100
   PROB_HEAD = 0.4
   CONST_GAMMA = 1.0
   CONST_EPSILON = 1e-3 # used for value iteration termination
   states = np.arange(0, CONST_GOAL + 1)
   stateValues = np.zeros(states.shape) # 1-99 total 99 number of states
   stateValues[100] = 1.0 # goal state
   historyStateValues = np.zeros((10,CONST_GOAL + 1))
   policy = np.zeros(states.shape)
   
   def getPossibleActions(capital):
       actions = []
       if capital <= 50:
           for i in range(0, capital + 1):
               actions.append(i)
       else:
           for i in range(0, 100 - capital + 1):
               actions.append(i)
       return actions
   
   def updateStateValue(state, action):
       newValue = PROB_HEAD * (0.0 + CONST_GAMMA *stateValues[state + action] ) + (1.0 - PROB_HEAD) * (0.0 + CONST_GAMMA * stateValues[state - action]) 
       return newValue
   
   def main():
       iteration = 0
       delta = 1e6
       while delta >= CONST_EPSILON:
           iteration += 1
           delta = 0.0
           previousStateValues = stateValues.copy()
           for capital in states:
               possible_stakes = getPossibleActions(capital)
               currentStateValue = stateValues[capital]
               maxValue = -math.inf
               for action in possible_stakes:
                   newStateValue = updateStateValue(capital, action)
                   # if iteration == 7:
                       # print("iteration:", iteration, "capital:", capital, "possible_stakes:", possible_stakes, "action:", action, "newStateValue:", newStateValue)
                   if newStateValue >= maxValue:
                       maxValue = newStateValue
                       stateValues[capital] = newStateValue
                       policy[capital] = action
               
               delta = max(delta, abs(stateValues[capital] - currentStateValue))
           historyStateValues[iteration % 10] = stateValues.copy()
       # plot
       fig, ax = plt.subplots(2, 1, figsize=(10, 10))
   
       ax[0].xaxis.set_major_locator(MultipleLocator(5))
       ax[1].xaxis.set_major_locator(MultipleLocator(5))
       # first plot
       axis_x = states
       colors = plt.cm.tab10.colors[:10]
   
       for k in range(iteration - 1):
           axis_y = historyStateValues[k]
           ax[0].plot(axis_x, axis_y,dashes=[2,2,5,2], label="iteration: " + str(k + 1), color=colors[k % 10])
       ax[0].legend(handlelength=4)
       ax[0].set_ylabel('value')
       ax[0].set_title('state-value')
       ax[0].grid()
       
       # second plot
       ax[1].set_ylabel('policy')
       ax[1].set_title('state-policy')
       ax[1].grid()
       ax[1].stairs(policy[0:CONST_GOAL], states)
       plt.show()
   
       # print("Final state values: ", stateValues)
       # print("Final policy: ", policy)
       
   
   
   
   if __name__ == "__main__":
       main()

上面的代码运行结束，可视化得到价值迭代过程和最优策略：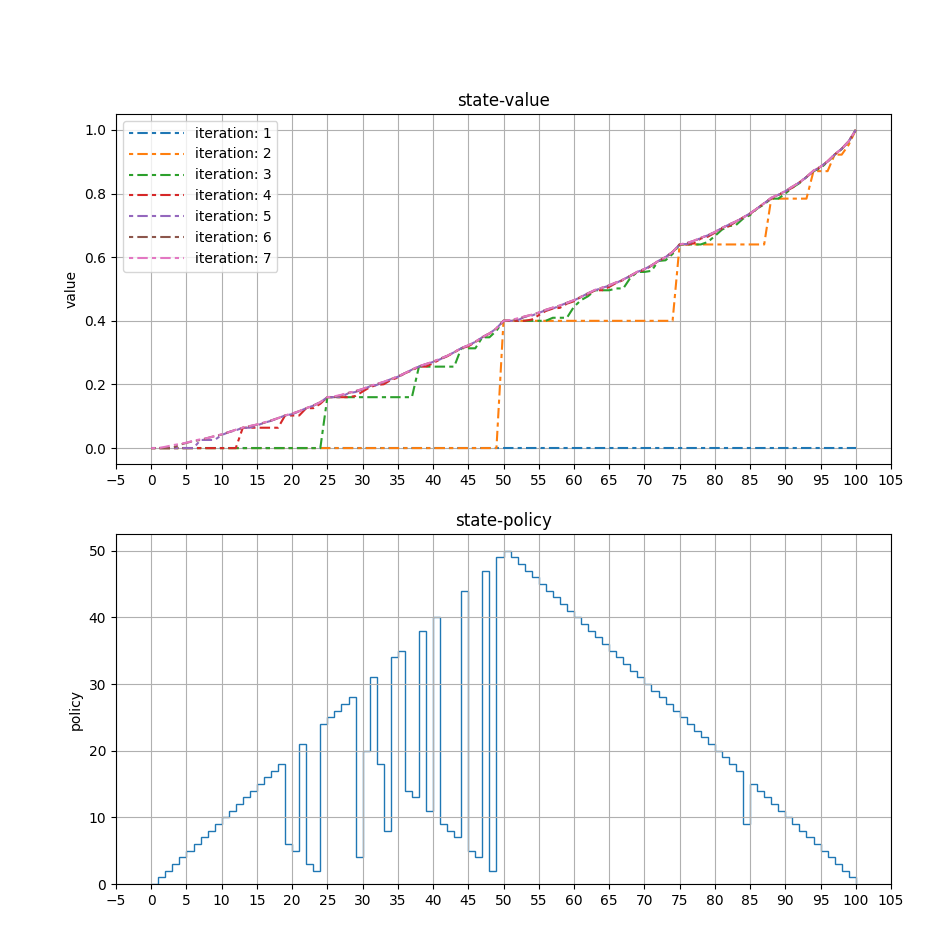

4.5 异步动态规划(Asynchronous Dynamic Programming)

这部分着重讲到了当面对现实问题的时候，状态的数量很庞大，可能采取的动作也很庞大，在这样的情况下，就算使用状态迭代的方法，也会造成很重的计算负担，实时性很差。异步动态规划可以解决这个问题。在计算的时候，可以选择性地保留一些状态，对这些状态进行迭代。 这部分并没有说具体的相关算法，但是提到了agent可以根据自己的经验，有选择地对某些状态进行迭代更新。后续应该会有相关的算法。

4.6 广义策略迭代(Generalized Policy Iteration)

是一个泛指，指代策略评估(Policy Evaluation)和策略改进(Policy Improvement)的交互过程。可以是顺序进行，也可以是融合在一起进行。

对立性：策略评估是认知的过程，即对当前的策略进行“客观”的分析，通过状态价值函数体现出来；策略改进，是打破策略评估的结果，在现有的策略框架下采取其以外的行动重新构建一个新的策略框架，这个时候，策略评估就需要针对新的策略进行重新分析。 所以说，对立体现在策略评估想要维护当前的现状，而策略改进想要打破现状，追求更高的状态价值。

合作性：没有策略评估，策略改进是没有依据的，因为策略评估给出了当前的状态价值，相当于给出了参考。没有策略改进，策略评估和现实世界距离太远，评估结果根本体现不出来现实世界的意义。

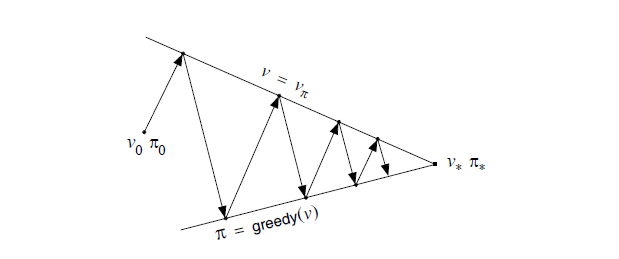
正如作者解释下面这张图，上面的策略评估这条线，代表为了找到真实的状态价值函数而做出的努力，下面的策略改进这条线，为了找到使得状态价值函数最大化的策略而做出的努力，两条线在不同的方向上面发展，最后发现各自做出的努力所取得的进展很小()的时候，就当作两条线相交，此时策略最优，状态价值函数最客观。

到这里，我突然想起来有人提过，强化学习就像一个自动控制系统当中的PID控制器，先通过反馈得到期望和状态的差，然后采取行动改变执行器的输出，接着反馈发生变化，再计算新的期望和状态的差(通常情况下，这个差会变小，假设期望值不变)。

Two Lines