学习RL(二)

第四章节 动态规划

4.1 策略评估

讨论的是如何在已知策略的情况下计算状态价值函数，从而得到采用该策略的价值有多大。

在DP当中policy evaluation的评估首先要计算状态价值函数，也就做prediction problem。

这里讨论的是如何计算状态价值函数，该函数是从初始的状态迭代计算的，不能无限制地一直迭代下去，这样严重影响实时性，所以上图提出了一种停止计算的终止条件。

还有一个具体的细节：提到了两种迭代的方式，一种是维护上一次所有状态的数组和当前状态的数组，计算当前的状态的时候只参考上一个状态的数组，还有一种是直接将上一次的数组某个状态更新了，其他状态的计算直接用更新了的。后面的讨论默认都是基于第二种方式。

4.2 策略改进

讨论的是如何在已知策略的情况下，如何改进策略，使得策略的价值更高。这里强调的单个状态下所有策略的局部最优—[代码实现过程中遇到的理解问题](### 代码实现过程中遇到的理解问题)

想法的来源是在状态为s的情况下，遍历所有可能采取的行动，看看哪种行动的状态-行动价值最高，那么，当后面遇到状态为s的时候，就直接采取这个行动。所以，对比于之前的策略，其实当前的策略已经变了，因为的概率分布发生了变化。所以这种策略叫做贪心策略。这种策略在对action做取舍选择的时候，只参考了之后一次更新的状态，并没有考虑更长远的更新状态。

4.3 策略迭代

步骤2里面，对当前的policy进行评估；步骤3里面，遍历每一个状态，针对该状态遍历每一个行动，找到能够使得状态-行动函数取值最大的那个或者那些行动，重新根据s生成关于a的概率分布函数，如果该函数和当前的一致，说明当前状态s已经找到了最优策略，开始下一个状态最优策略的寻找；如果修改

上图的两个关键是：在Policy Evaluation阶段，利用当前策略更新，在Policy Improvement阶段，利用更新的 去寻找使得当前行动价值最大的行动。

知识点应用： Jack's Car Rental Problem

研究如何运营A和B两地的车辆，首先需要实验当A和B之间不转运车辆的情况下，A和B保留车数量和收益的关系。

这个例子非常好地帮我我们理解了遇到一个问题，如何抽象状态，抽象行动，构建策略和寻找到最优的策略。

行动

为了应用动态规划的方法，需要设定行动和状态，这里的行动是转运车辆的数量，描述为如下的形式：
假设从A到B转运车辆的数量设定为 , 当表示运送辆车从A到B，当表示运送辆车从B到A。

状态价值

可以想象成一个二维的地图，y轴上面是A地的车辆数量分布，x轴上面是B地的车辆数量分布，z轴是的高度，就是该状态下的收益或者价值(value) 参见下面的热力图的最后一张子图。
updateStateValues函数利用给定的行动遍历当前状态进行了Bellman方程的应用计算得到新的状态价值。

策略

策略可以想象成一个二维地图，x轴上面是A地的车辆数量分布，y轴上面是B地的车辆数量分布，z轴代表行动当中的某一个取值。

策略评估和策略改进

初始的策略可以选择是到了晚上不移动任何车辆，然后在状态上遍历所有可能的行动来更新状态收益，从状态收益当中选择一个最大的，从而对应的那个行动就变为该状态下的行动，从而完成对当前状态的策略改进，这里采用了贪心的改进策略，后续应该会遇到更加合理的改进方法。

numberofMoving这个二维数组存储了最新的策略。

Poisson分布: 在一个采样间隔里面，一个随机事件发生的次数有一个期望值 ，那么，当事件在该采样周期内发生了 次的概率为：

代码实现过程中遇到的理解问题

1. 策略理解不够深入，没有创建策略的二维数组来存储策略。
2. 策略的评估没有做从初始的策略和状态直接进行策略改进，查看输出结果不对。– 应该先做好策略评估，也就是遍历所有状态，按照初始的策略进行迭代，得到在该策略下的状态价值函数，在这里就是二维的数组stateValues,然后拿着这个更新了的数组来找到最优的行动。
3. 跟gridworld相比，这次的不确定的是策略，具体来说就是当处在某一个状态，例如A处存留10辆车，B处存留7辆车，到了晚上应该从A到B运输多少量车，是需要尝试的，通过不同的尝试之后，就得到第二天不同的A和B的留存车辆状态，通过策略评估得到状态价值函数，从状态价值函数找到最优的行动。
4. 在更新状态价值的函数当中updateStateValues, 这个函数关心的问题是从给定状态转移到新状态（有很多种可能性，例如A点出租了2台车，有3台车归还拥有一个概率, A点出租了5台车有6台车归还拥有不同的概率,但是都造成到了晚上A点拥有相同的剩余车数量，像这种情况需要对泊松分布的高概率事件数量进行遍历，把造成晚上都是某个数量车的所有情况的概率加权考虑进去。这个泊松分布的高概率事件数量如何定义？从二维分布图上，可以指定一个高于0的水平直线，高度是,代表了接车或者还车数量为n的事件发生概率低于0.01的n统统排除在外，只考虑比其发生概率更高的n），这个转移是通过行动来实现的，所以在这个函数当中，需要传入行动，然后根据行动来计算状态价值的更新。
5. 还是在updateStateValues函数当中，当天的借车还车数量是很多种可能性的，，仔细看这个条件概率里面的是确定的，也就是前一天晚上的挪车成本在第二天早上就确定了，不确定的部分是第二天一整天下来的借车数量–利用概率对这部分的收益求平均值。所以updateStateValues函数当中的reward不应该按照下面的计算方法加入到概率的加权求和。

reward = (rentalNumA + rentalNumB) * CONST_SINGLE_REWARD - abs(action) * CONST_MOVING_COST

而是应该
reward = (rentalNumA + rentalNumB) * CONST_SINGLE_REWARD
最后再把前一天晚上的成本加入到里面去。

再来把Bellman equation列在这里, 公式中是确定的，所以采取行动的成本就确定了，但是第二天的白天状态切换的过程是随机的，满足泊松分布，这部分的收益是需要求期望的。

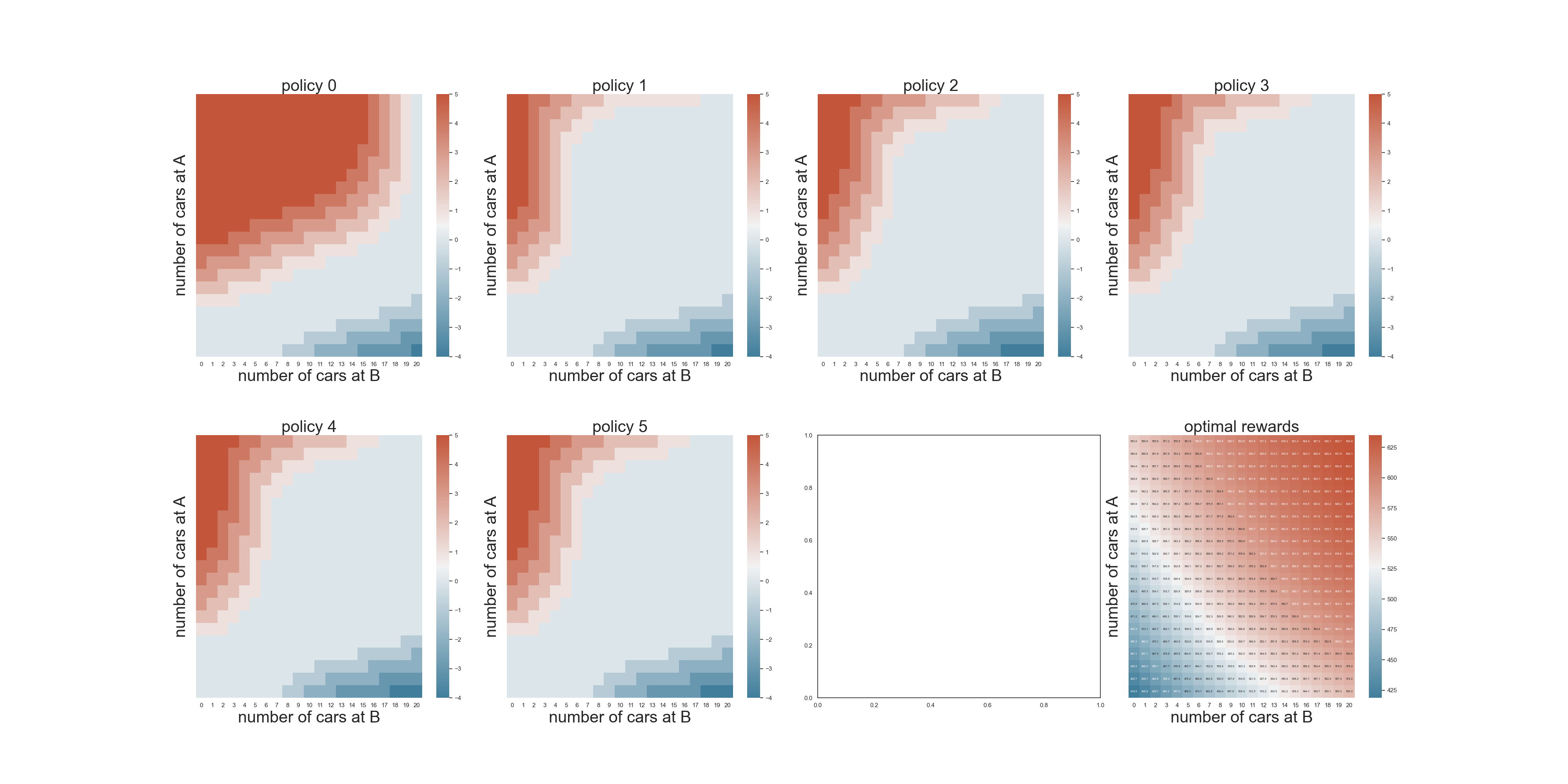
Exercise 4.5,Jack的员工可以下班帮忙开车和停车场空间限制场景加进来。

需要改动的地方在于价值函数，也就是updateStateValues当中。

最终的计算结果如下：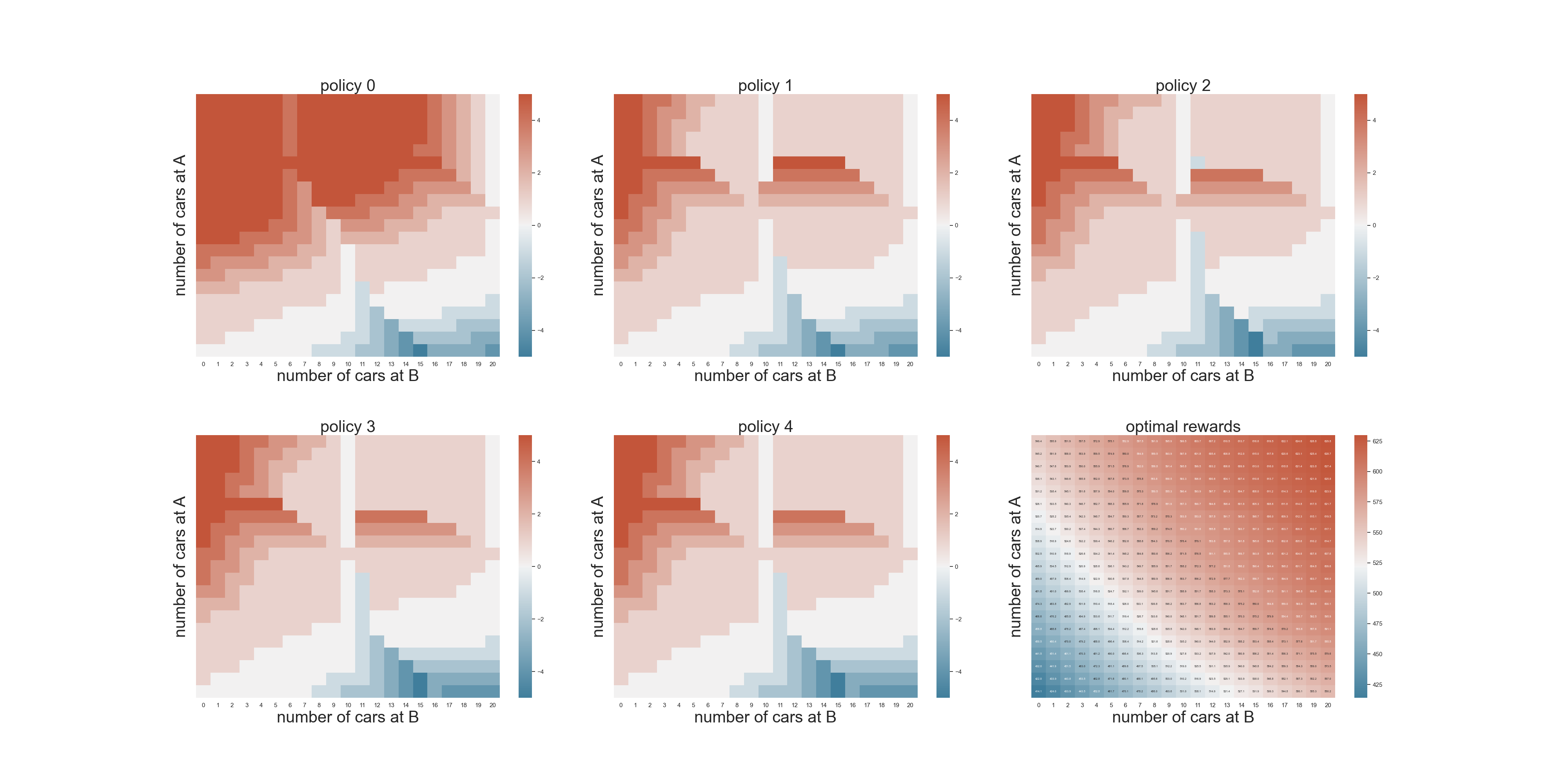

JCR的python代码

外部参考

最终的结果展示采用热力图的形式，使用了seaborn库，参考了这个链接：
https://seaborn.pydata.org/examples/many_pairwise_correlations.html

学习时间线索

• 2024年10月

  • 读Sutton’s Book 第四章节
  • 做了一些笔记，试图理解其中的概念。

• 2025年1月

  • 自己实现Jack’s Car Rental 问题
  • 暴露出来了[代码实现过程中遇到的理解问题](### 代码实现过程中遇到的理解问题)

• 2025年2月

  • 春节回来完善JCR
  • 核对结果和画图展示