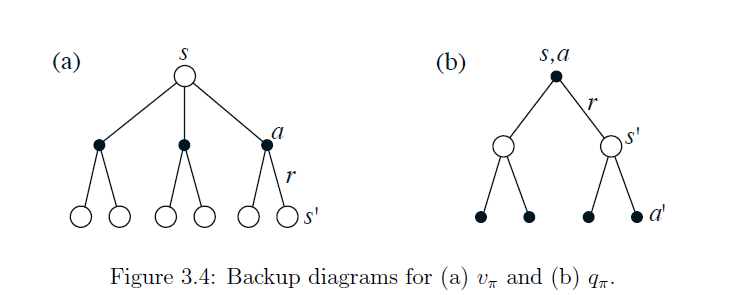
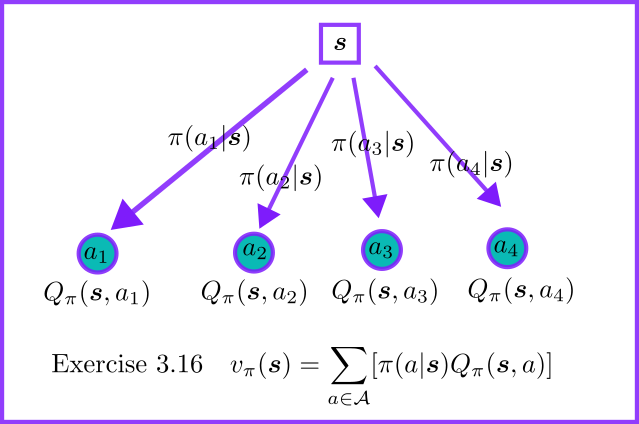
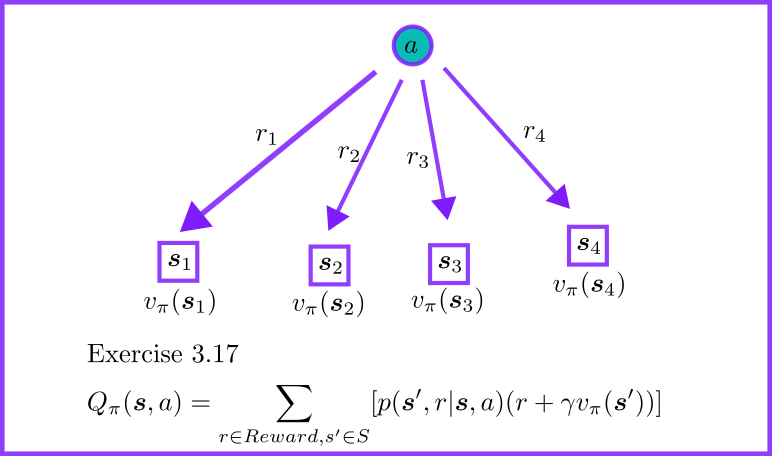
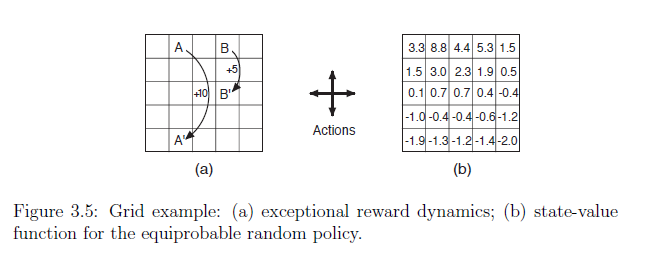
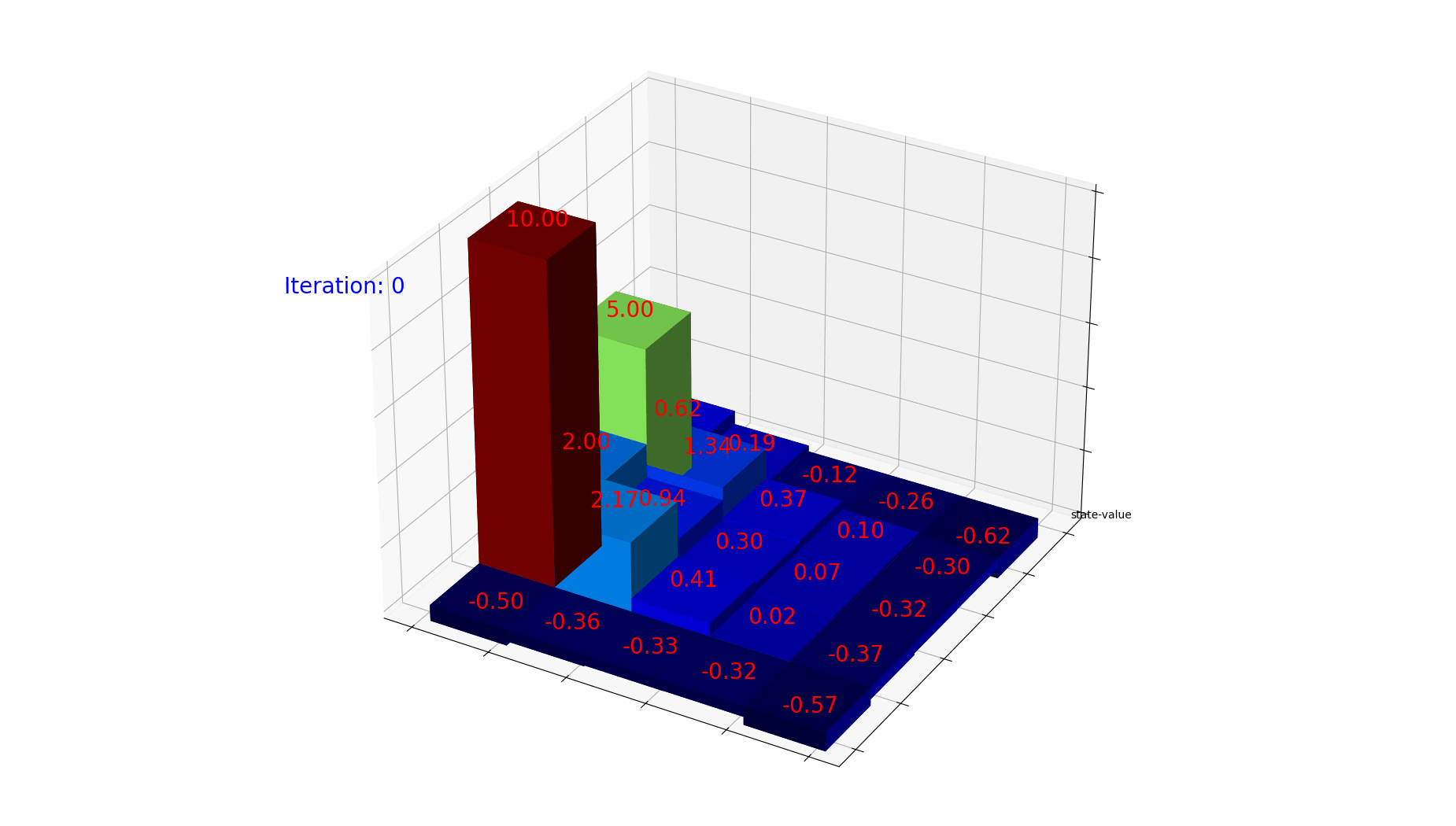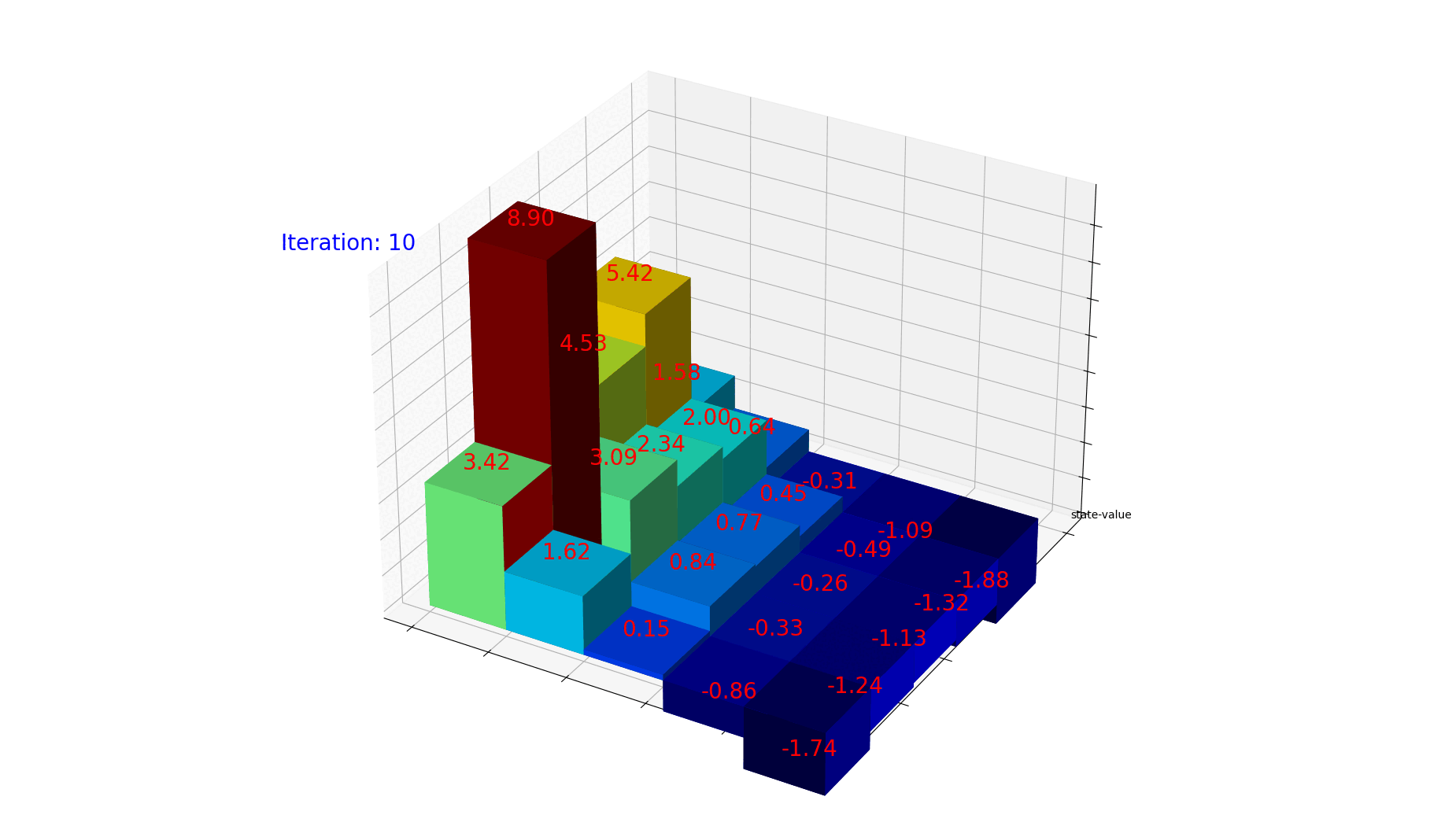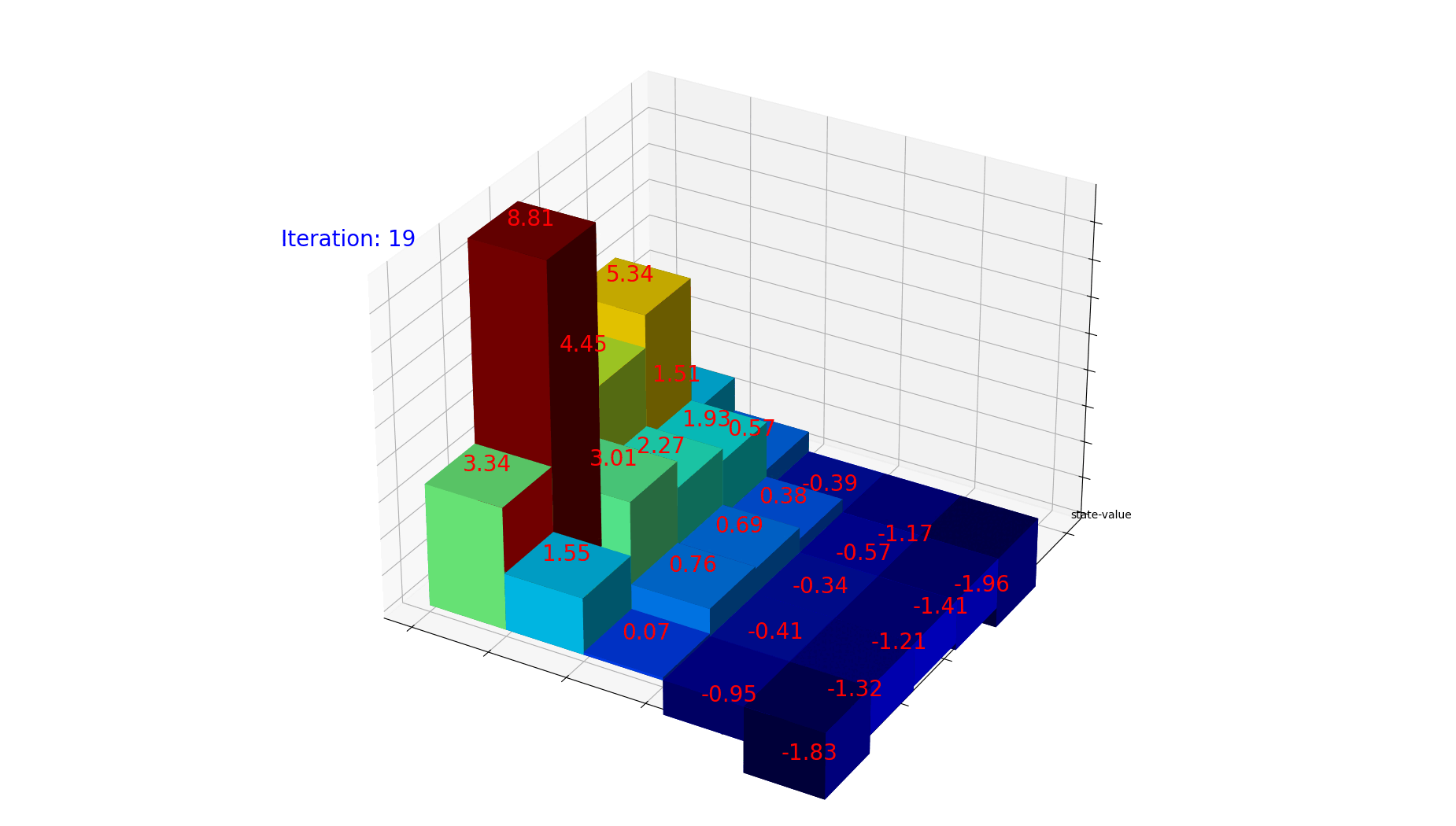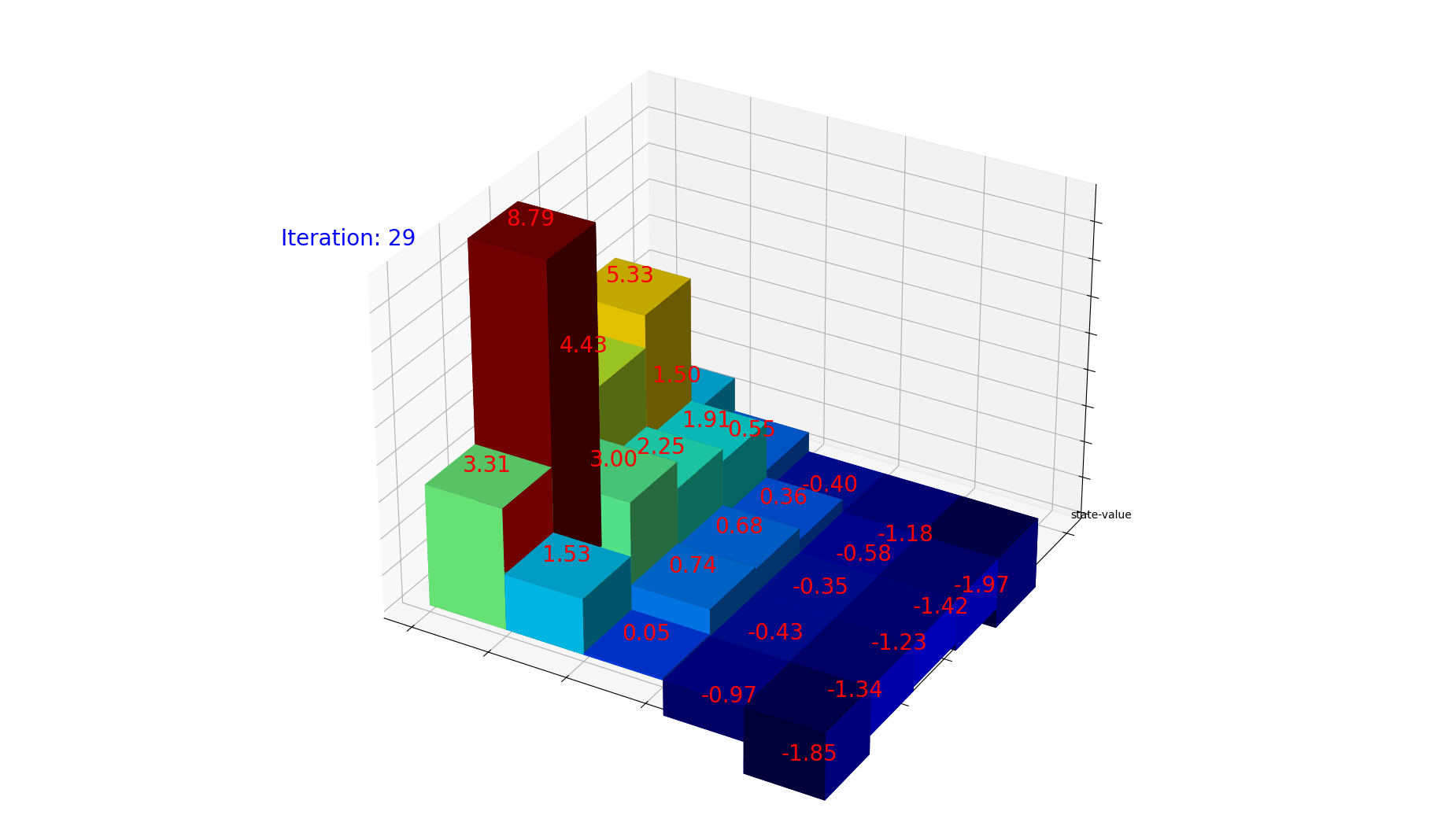
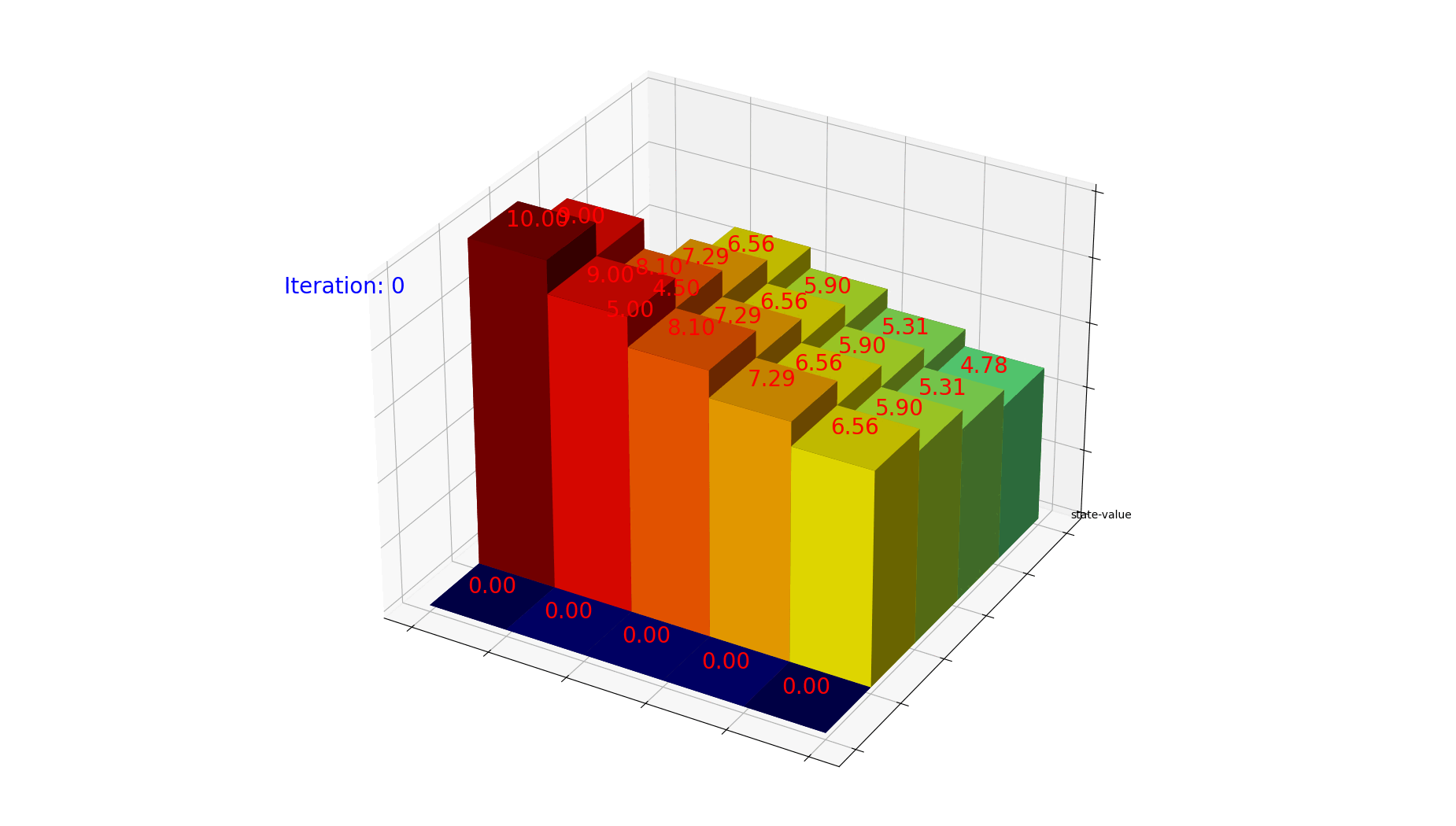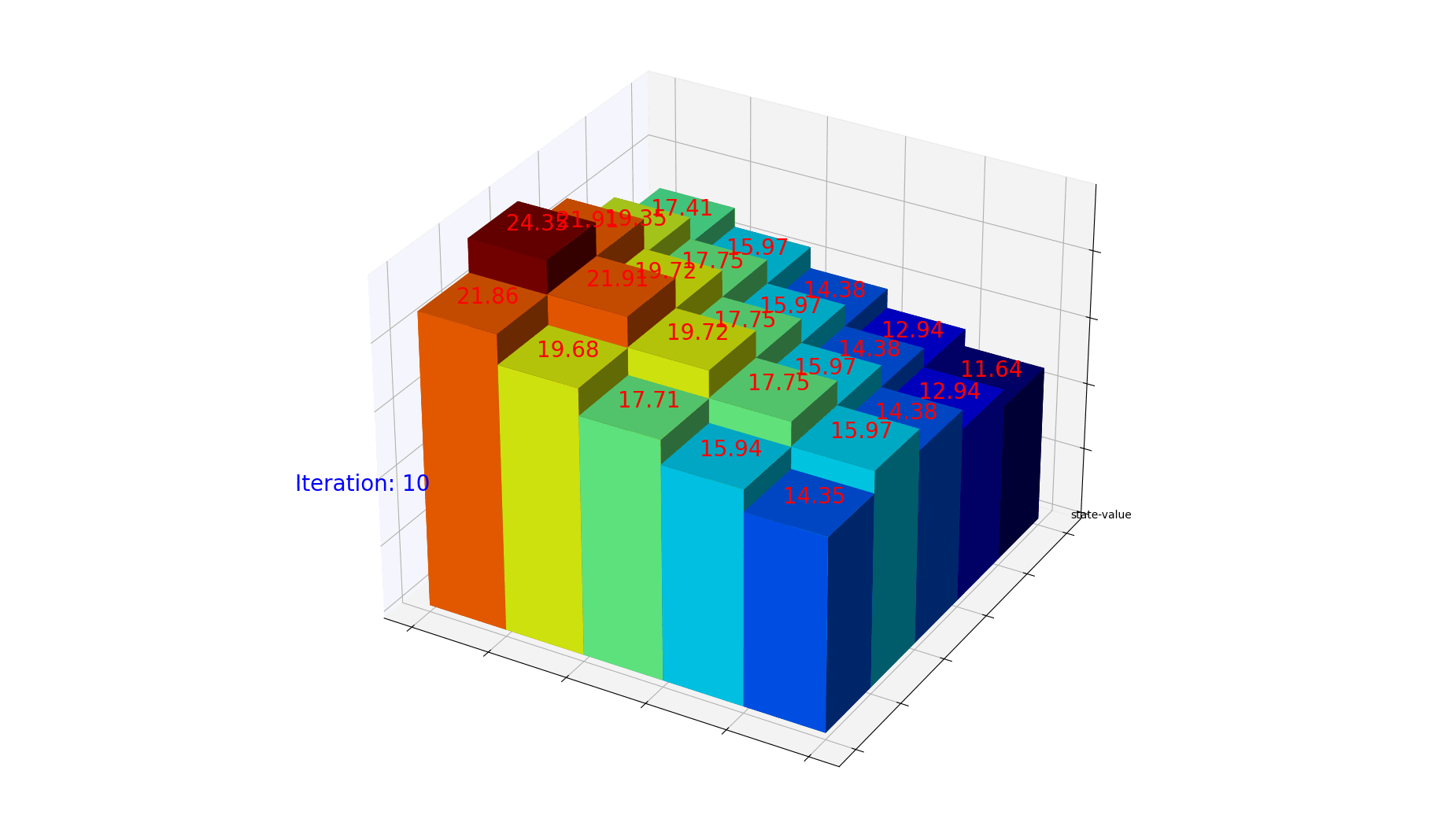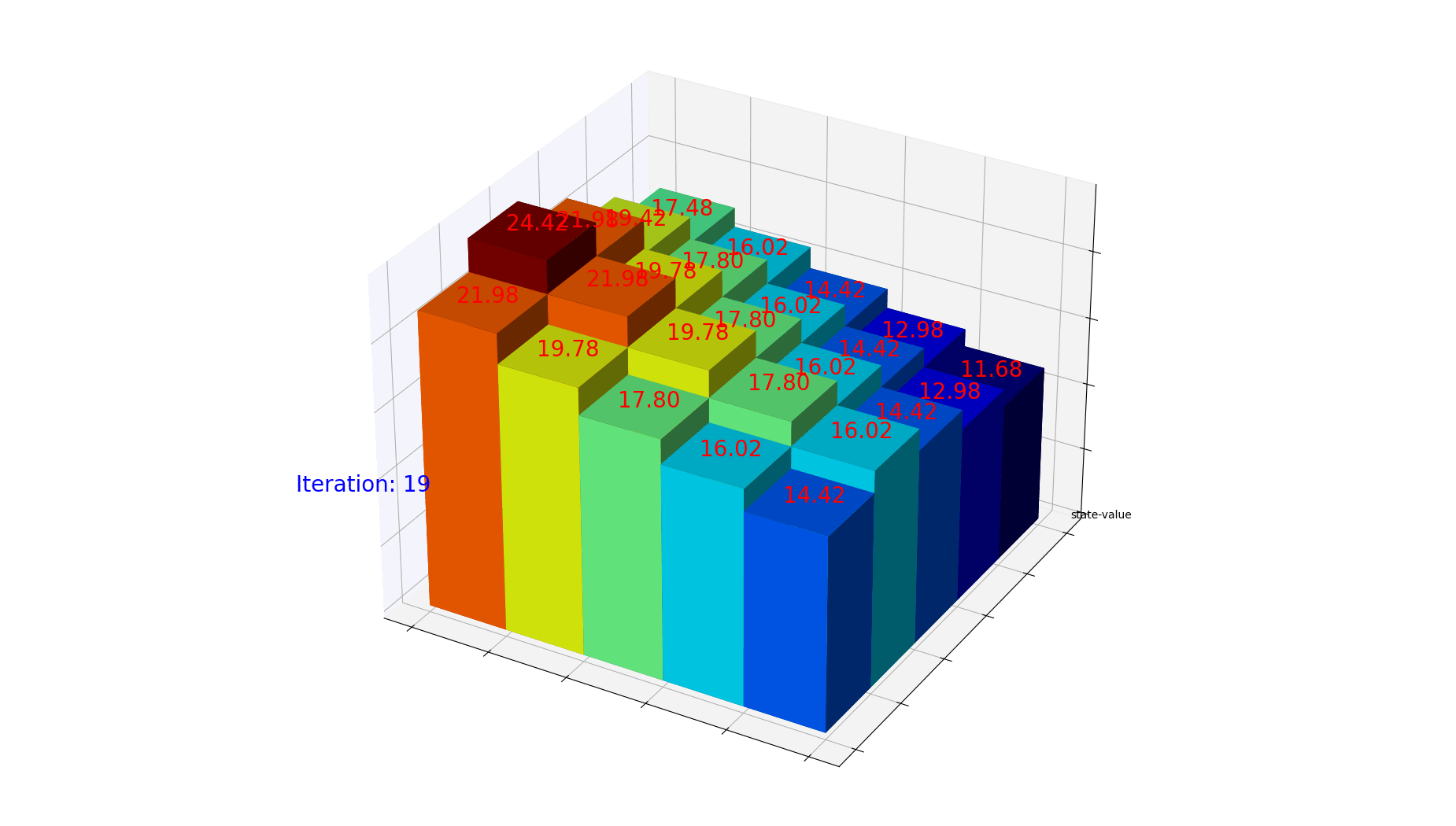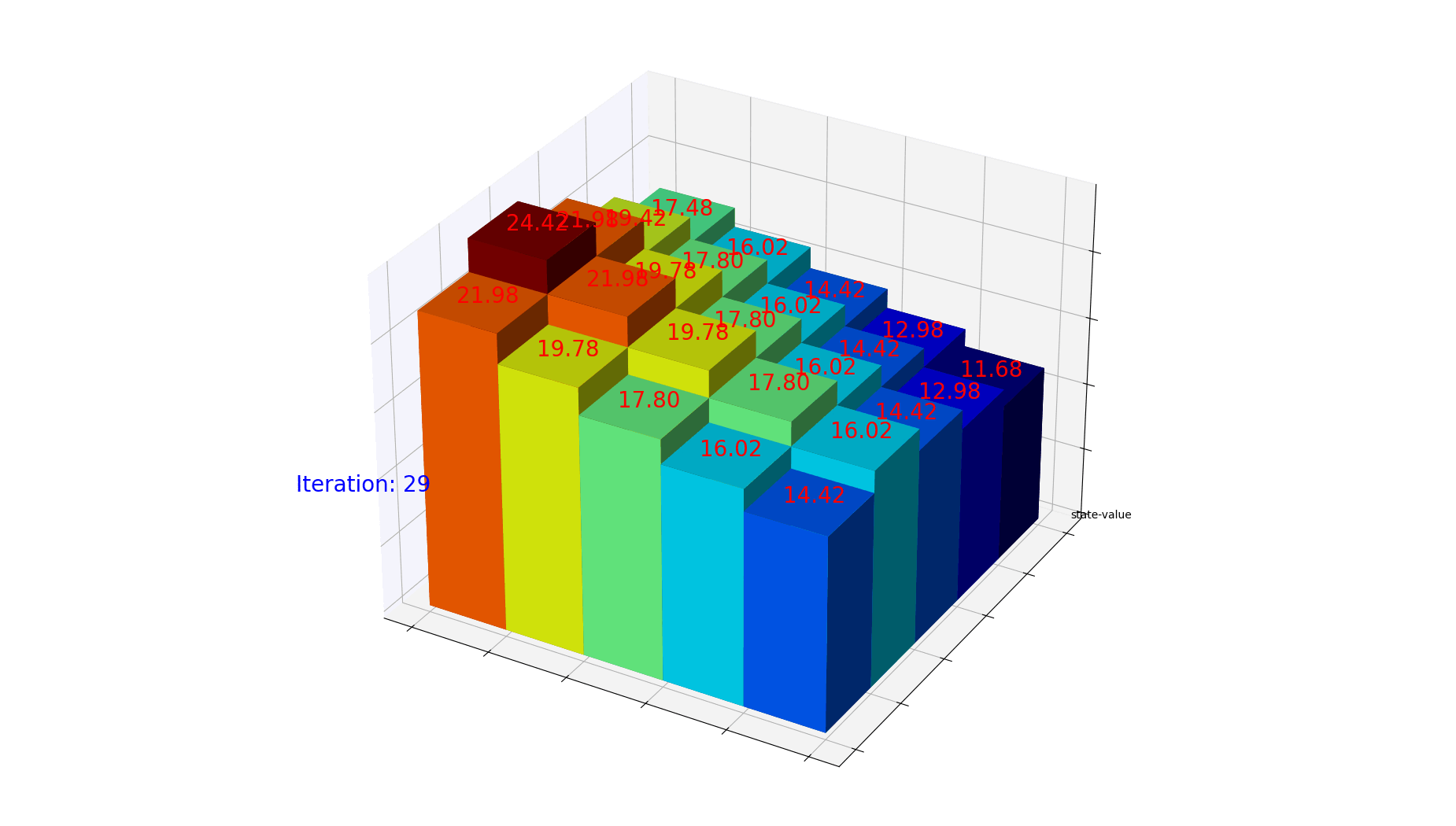
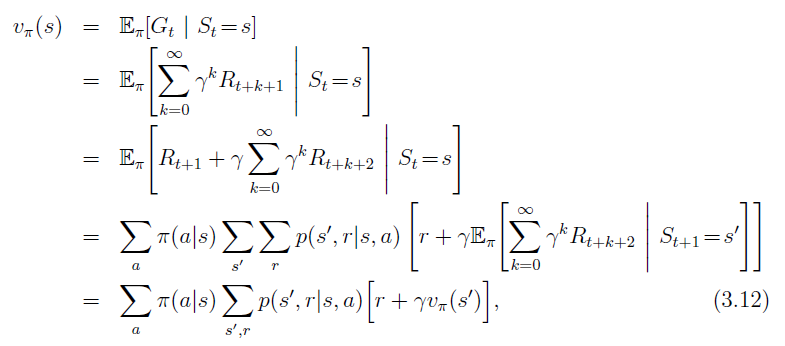1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
| import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.animation as animation
import matplotlib.colors as colors
import matplotlib.cm as cm
from matplotlib.animation import ImageMagickWriter
plt.style.use('_mpl-gallery')
N = 5
x = [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5]
y = [1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5,1,2,3,4,5]
z = np.zeros(25)
dx = np.ones_like(x)*0.5
dy = np.ones_like(x)*0.5
gridValues = np.zeros((5, 5))
gamma = 0.9
OutReward = -1
InNormalReward = 0
InSpecialReward_A = 10
InSpecialReward_B = 5
iteration = 30
dz = np.zeros((iteration,25))
initdZ = np.zeros(25)
def getOptimalPolicyDirections(row, colunm):
if (colunm == 0):
if(row == 0):
return [0,0,0,1]
elif(row == 1):
return [1,0,0,1]
elif(row == 2):
return [1,0,0,1]
elif(row == 3):
return [1,0,0,1]
elif(row == 4):
return [1,0,0,1]
elif (colunm == 1):
if(row == 0):
return [1,1,1,1]
elif(row == 1):
return [1,0,0,0]
elif(row == 2):
return [1,0,0,0]
elif(row == 3):
return [1,0,0,0]
elif(row == 4):
return [1,0,0,0]
elif (colunm == 2):
if(row == 0):
return [0,0,1,0]
elif(row == 1):
return [1,0,1,0]
elif(row == 2):
return [1,0,1,0]
elif(row == 3):
return [1,0,1,0]
elif(row == 4):
return [1,0,1,0]
elif (colunm == 3):
if(row == 0):
return [1,1,1,1]
elif(row == 1):
return [0,0,1,0]
elif(row == 2):
return [1,0,1,0]
elif(row == 3):
return [1,0,1,0]
elif(row == 4):
return [1,0,1,0]
elif (colunm == 4):
if(row == 0):
return [0,0,1,0]
elif(row == 1):
return [0,0,1,0]
elif(row == 2):
return [1,0,1,0]
elif(row == 3):
return [1,0,1,0]
elif(row == 4):
return [1,0,1,0]
for num in range(iteration):
for i in range(5):
for j in range(5):
up_grid_value = gridValues[i-1, j] if i > 0 else None
down_grid_value = gridValues[i+1, j] if i < 4 else None
left_grid_value = gridValues[i, j-1] if j > 0 else None
right_grid_value = gridValues[i, j+1] if j < 4 else None
fourBasicDirections = [up_grid_value, down_grid_value, left_grid_value, right_grid_value]
cur_value = 0
directionNum = 0
if i == 0 and j == 1:
cur_value = cur_value + InSpecialReward_A + gamma * gridValues[4, 1]
elif i == 0 and j == 3:
cur_value = cur_value + InSpecialReward_B + gamma * gridValues[2, 3]
else:
for dirIndex in range(4):
directionNum = directionNum + getOptimalPolicyDirections(i, j)[dirIndex]
if (fourBasicDirections[dirIndex] == None):
cur_value = cur_value + (OutReward + gamma * gridValues[i,j]) * getOptimalPolicyDirections(i, j)[dirIndex]
else:
cur_value = cur_value + InNormalReward + gamma * fourBasicDirections[dirIndex] * getOptimalPolicyDirections(i, j)[dirIndex]
if directionNum > 0:
cur_value = cur_value / directionNum
gridValues[i, j] = cur_value
dz[num] = gridValues.ravel()
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
fig.set_size_inches(18.5, 10.5)
ax.set(xticklabels=[],
yticklabels=[],
zticklabels=["state-value"])
def update_plot(frame_number, zarray, plot):
plot[0].remove()
bottom = np.zeros_like(zarray[frame_number])
offset = zarray[frame_number] + np.abs(zarray[frame_number].min())
fracs = offset.astype(float)/offset.max()
norm = colors.Normalize(fracs.min(), fracs.max())
color_values = cm.jet(norm(fracs.tolist()))
plot[0] = ax.bar3d(x, y, bottom, 1, 1, zarray[frame_number], color=color_values, shade=True)
for text in ax.texts:
text.set_visible(False)
ax.text3D(0, 0, 10, "Iteration: " + str(frame_number), fontsize=20, color='blue')
for each_x, each_y, each_z in zip(x, y, zarray[frame_number]):
label = format(each_z, '.2f')
ax.text3D(each_x + 0.3, each_y + 0.3, each_z + 0.2, label, fontsize=20, color='red')
plot = [ax.bar3d(x, y, z, dx, dy, initdZ, shade=True)]
animate = animation.FuncAnimation(fig, update_plot, iteration, interval=2000, fargs=(dz, plot))
animate.save('state_value.gif', writer=ImageMagickWriter(fps=2, extra_args=['-loop', '1']))
plt.show()
|
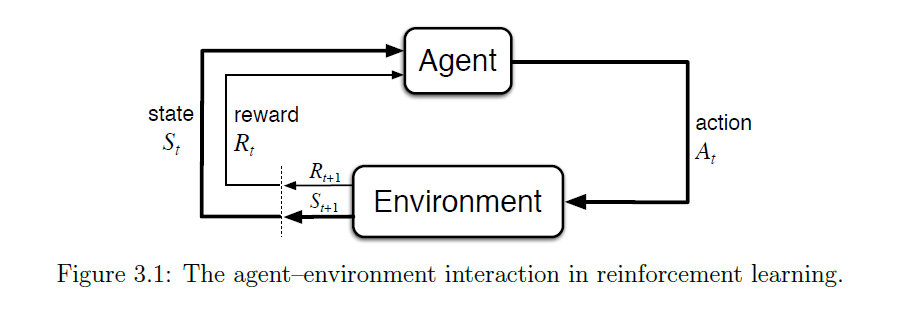
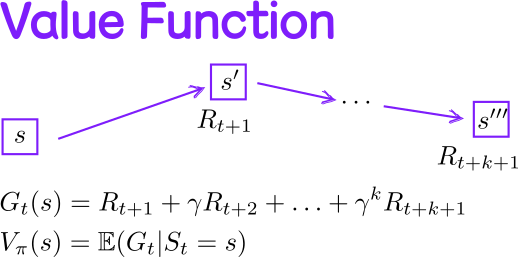 参考:A
(Long) Peek into Reinforcement Learning Action
Value:类似于 Value Function。
参考:A
(Long) Peek into Reinforcement Learning Action
Value:类似于 Value Function。