卡尔曼滤波器学习笔记(二):随机过程和线性卡尔曼滤波器
随机过程的模型建立
一般地,我们研究的随机过程是一个动态的系统(Dynamical Systems).
其中,
为了简化我们对系统的建模,首先把时间和系统参数对系统迭代的影响忽略掉,简化上面的等式:
(
上面的等式仍然不是很理想,因为经常性的,
那么,需要对(
(
状态转移方程
(
(
非线性的系统状态转移矩阵是根据系统的雅可比矩阵来确定的,每次迭代都会变。后续需要确认是不是这样。
到目前为止,根据系统的物理定律我们在没有测量的状态下得到系统状态是如何迭代的,但是需要注意(
随机过程的贝叶斯后验概率分布推导
根据第一讲贝叶斯滤波的基本思路,系统迭代的过程中,需要有测量数据做融合,从概率论角度讲就是测量数据
在推导之前,需要非常明确这几条:
- 状态向量迭代的过程虽然是离散的,例如
- 在不同的时刻下,先验、后验分布都在变化,先验分布变化是因为系统因为物理、化学等规律随之前的状态产生了新的变化 -- 就是由状态转移方程描述的。
后面的公式当中,
状态转移的概率分布推导
对
到这里很容易迷茫不知道怎么办,看
继续推导得到:
这里,条件概率变为了当
观察(
概率分布函数是概率密度函数的原函数,根据微积分第一基本定理,对
当
测量更新的概率分布推导
这里首先需要给定测量出来的向量作为随机变量
再次列出来连续随机变量的贝叶斯公式:
测量向量
后验概率分布如下:
首先是似然概率:
条件概率的条件
然后是边缘概率。
到这里,我最开始对于为什么需要把分母的那个边缘概率展开为全概率是不理解的,它其实就是一个不为零的常量,直接放在那里不是就可以了么?
在 Kalman and Bayes Filters in Python3.12
章节讲到了这个量叫做evidence,就是不考虑当前状态在哪里的情况下,测量值出现
那么问题又来了,我们怎么寻找那个全概率的“基底”呢?就是上一篇文章中说的
令
得到:
因为在实际计算的过程中,预测步骤得到的
卡尔曼滤波器
引入期望的几何意义
(
Kalman在1960年发表的论文当中,首先论证了如何最小化估计和真实值之差在给定测量值条件下的期望,解就是状态在测量条件下分布的期望。
论文中还讲了正交投影,把测量空间内的随机变量分解为若干个单位正交的随机变量的线性组合,定义随机变量正交需要满足乘法期望为零。所以,任意随机变量可以分解为两部分:一部分属于测量空间,一部分属于正交于测量空间。
测量空间的表示
正交空间的表示
论文中证明了在正交空间内的任意随机变量,都和测量空间内的随机变量正交,下面的符号代表了正交空间内的随机变量:
状态变量的最优估计就是向测量空间做正交投影得到的新的随机变量
论文中证明了这一点。在阅读论文的过程中,我发现,推导过程和模型很类似于最小二乘法在向量空间中的推导,所以下面的描述是对照最小二乘和随机变量的最优估计来进行。
在我之前的一篇文章《投影矩阵和最小二乘》中,已知空间当中的一些点,如何找到一条直线使得这条直线到每一个已知点的距离最小,这个问题和现在的随机变量估计问题有很深的类似关系。
- 给定的已知点就是这里的测量,而且不同时刻
- 最小化一个目标函数,在最小二乘当中,最小化的是误差绝对值的求和,在这里最小化的是估计出来的随机变量
- 最小二乘当中,为了求出那条直线,需要确定两个参数
- 如果随机变量
- 得到了投影之后的随机变量
论文当中的演进思路
Optimal Estimates: 给定了一组测量值,如何最优估计出来带有噪声的测量值所测量的状态向量?Wiener指出状态估计问题就是需要使用概率理论和统计的方法来解决。论文当中的定理1,说的是对状态向量的最优估计(最优的意义是把估计量和实际量做差当作一个随机变量,然后对该变量求loss 一般是
Orthognal Projection: 讲的是给定一组测量值
Models For Random Processes: 讲的是对系统进行建模,最理想的情况是首先定义了一个时间原点,然后根据当前时间作为输入给出我们关心的系统输出和时间的数学表达式。这样的方法在实际应用当中不方便,人们更多关注的是基于现在的已知情况,求出当前情况下的系统输出是什么样子(状态转移方程)或者系统变化了多少(一阶微分方程),不管是前面的哪种,都属于一个迭代的描述,从而有了有一阶的微分方程,如果系统是线性的,可以把微分方程写成状态转移方程。但是,尽管我们可以得到状态转移方程,在实际应用当中,无法忽视系统迭代过程中噪声模型,人们也不可能列举所有可能的输入下系统输出的分布情况,但是人们可以统一做一组实验,就是在单位阶跃的输入下,系统随着时间如何变化,或者在均值为0的高斯扰动下,系统产生的输出的不确定度,这个不确定度使用了
Solution Of the Wiener problem: 讲的是从系统迭代的角度,在有状态转移方程、过程噪声协方差矩阵、测量向量和测量噪声协方差矩阵情况下,如何求解系统状态的最优估计。99%的情况下,新得到的测量值一定是携带了新的有用信息,从数学的角度来看,就是这个
这一步就是需要计算出卡尔曼增益矩阵的具体表达式。因为卡尔曼增益是
我理解的计算过程如下图:图中灰色椭圆代表了新的测量引入的额外信息
首先需要明确的是测量误差和经过预测的可观测部分和测量值之间的误差是不同的。
2025-06-04
Geometric
illustration of the Kalman filter gain and covariance update
algorithms - 下图左侧,
原始论文当中,其实并没有提到从几何的角度理解,但是重点强调了垂直于
最优估计一定要落在
问题变为如何在已知一个点和一条线段的前提下,求出点到线段的最短距离--这个距离体现的就是卡尔曼估计的状态更新误差
适当理解右图的三角形:当三角形左边直角边变短(系统模型更精确):卡尔曼估计偏向系统的预测;当三角形右边直角边变短(测量噪声更小):卡尔曼估计偏向测量。
卡尔曼增益是从三角形左下顶点到垂足的线段和整个斜边的比例。
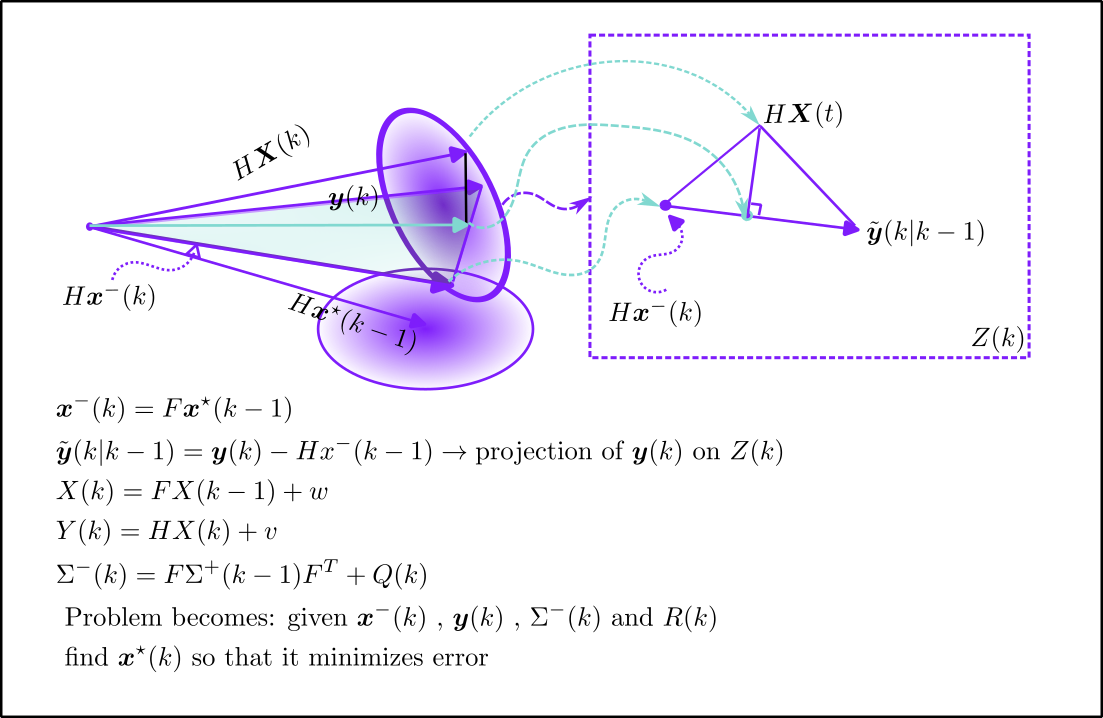
续2023-12-08:
可以用简单的几何关系来推导一下:
推出:
不可观测部分:
推出:
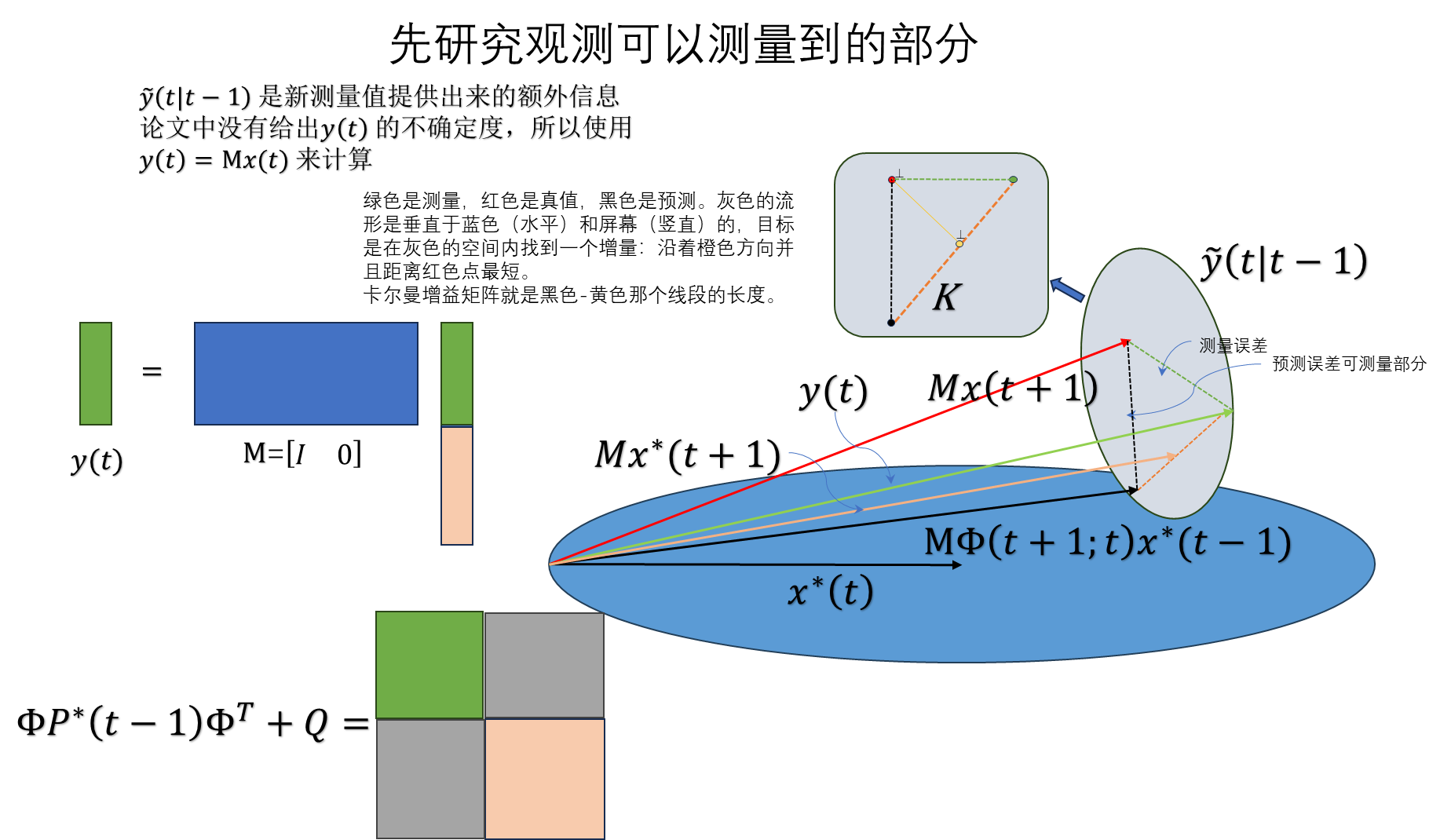
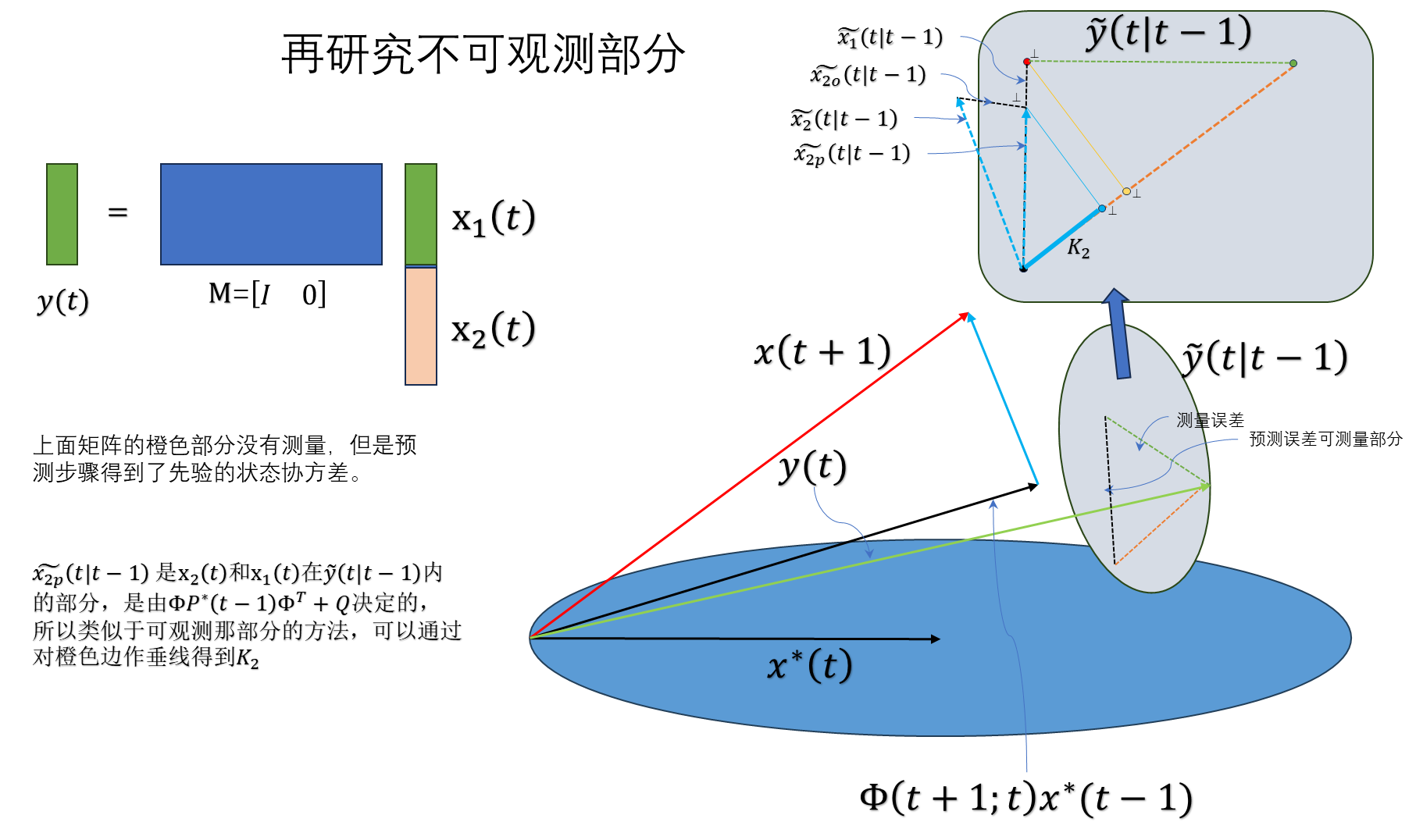
有了直观的几何理解,后面的具体推导部分,就比较容易理解和建立对应关系了。
具体的推导过程
就是假设随机变量的分布是高斯的,也叫做正态分布,这个分布有如下的特性:
- 使用
- 假设过程噪声
所以过程噪声的概率密度函数写为:
测量噪声的概率密度函数写为:
由于我们需要从第
(1)随机变量
(2)最优估计当中的损失函数定义为
高斯分布概率密度函数代入:
上面的推导得到结果:
- 卡尔曼滤波的五个公式。
(
卡尔曼滤波和最小二乘的关系
2025-5-29
投影矩阵和最小二乘
-
最小二乘解决的是已知空间中有很多点,如何找到一条直线,能够保证这条直线到给定的所有点的距离最短,具体问题的形成过程参考上面的链接。
-
卡尔曼滤波解决的是:已知历史上很多的观测点,如何得到待估计的状态的最合理的值,这个最合理,Kalman定义出一个loss
function,就是实际上的状态(Ground Truth)
- 2)状态估计
- 3)背后有一个隐含的东西是:我们手头上拿到的观测其实代表了一个空间(这是客观存在的根本信息,比观测本身要有更好的质量,因为可以通过一些正交基
- 4)最小二乘里面最小化的是那个
- 5)卡尔曼先生用图形化的方法(其实就是最小二乘的模型),空间当中给定任意一个向量,其实就是待估计的状态
- 6)上面的描述过程,其实大部分是飘在天上~
- 7)如果我们联系上要研究的系统,
mathjax 写作遇到的问题
下标经常解析不出来,需要在下标前使用空格,例如f_{k-1}
写成f _{k-1}
参考文献
Data-Driven Science and Engineering -- Steven L. Brunton