卡尔曼滤波器学习笔记(一):概率论和贝叶斯滤波
感谢
点一个大大的赞! 经典教材的重新排版
文章中深蓝色字体表示摘录自该教材。
给老王点赞! 老王
这个作者真心用心地交互式展示数学和工程实践。 Kalman-and-Bayesian-Filters-in-Python
这篇容易让我们建立直觉的理解
背景知识
一本很有名的书,学习作者对内容的安排。  需要的预备知识:
需要的预备知识:
线性代数
概率,概率密度函数
离散变量贝叶斯滤波
连续变量贝叶斯滤波推导
学习心得
首先是概念理解,需要把概念代表的物理意义搞清楚:事件≠随机变量,随机变量是对事件的数量化描述,事件是随机变量的取值,随机变量的取值可以是一个数,也可以是一个向量。概率密度函数是对随机变量的取值的概率分布的描述,概率密度函数的积分就是概率。概率密度函数的积分就是概率,概率密度函数的积分就是概率,概率密度函数的积分就是概率。重要的事情说三遍。
亲自手写公式推导一遍,在这个过程中会强烈加深对内部逻辑的理解,争取可以做到经过很长时间之后,你仍然可以随便拿一张纸开始从零推导
感觉基于贝叶斯的随机过程计算其实是在更新变量的概率分布,并不是直接计算最终你看到的数据,最后你得到的数据只是这个过程当中的附带产品。
上面这一条的感受里面说的计算过程,基础是全概率下的全部样本空间,像是在一个无限大的平面上(因为真实值的取值是无穷无尽的)时刻飘过一团云,这团云和云笼罩下的区域是本次计算的结果。
符号说明
一般性地,我们用
概率论回顾
随机变量
条件概率的定义: 某事件B发生的条件下,事件A发生的概率,记为
乘法公式:
全概率公式: 全概率公式是另一个很重要的公式,提供了计算复杂事件概率的一条有效的途径,使得一个复杂事件的概率可以通过简单的计算得到。
全概率公式:设
贝叶斯公式: 这个公式得到的前提是乘法公式和全概率公式。 设
体会:虽然我没有查找托马斯·贝叶斯发现这个定理的过程是不是因为实际的应用问题,因为在状态估计这个领域,具有非常强的适配性,我们可以把样本空间理解成状态变量的空间,
维基百科里面说这个方程的分母是
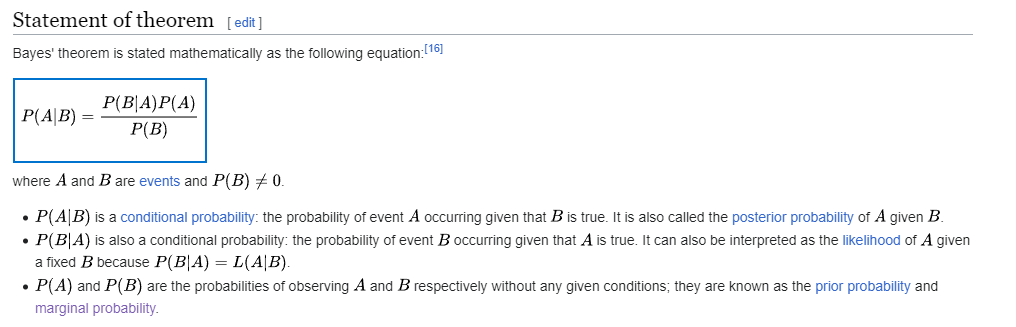
然后我看到了它说
在这里隐约感觉到:这里的论述和线性代数里面的空间向量怎么很类似?跟信号的傅里叶分解也很类似:全部都是把一个复杂的东西分解成一些简单的东西,然后再把这些简单的东西组合起来得到复杂的东西。这块简单的东西就是全样本空间下每一种样本的概率,类似于空间中的基向量,或者傅里叶变换中的基函数,然后这些基函数前面的系数就是权重或者是事件A和

最后再次用更好记忆的方式写一遍贝叶斯公式:
条件概率是概率论中一个既重要又实用的概念。 -- 1.4《概率论与数理统计》茆诗松
- pdf: probability density function, 概率密度函数
- cdf: cumulative distribution function, 累积分布函数
- 先验概率:就是人们根据自己系统的模型给出来的经验概率
- 后验概率:就是通过传感器本身的测量特性--传感器测某个状态得到的结果这个变量的概率分布和先验的概率分布,得到的对系统的状态变量条件概率
- 似然概率:是一个条件概率,意思是当真实值取值为
的时候,测量值取值为 的概率, (这里默认测量值测量到的就是真实值)
我觉得还需要加一个边缘概率:边缘概率就是全概率公式对于某一个事件的应用,就是基于所有可能的状态量,测量得到
这里有一个问题抛出来:假如先验概率变了,后验概率会变吗?似然概率会变吗?边缘概率会变吗?
我的回答是似然概率不变,边缘概率会变,因为从全概率公式就可以知道那些“基底”变了,前面的参数没变,整个求和就变了,所以后验概率也变了。
Kalman-and-Bayesian-Filters-in-Python

桥梁
在纯讲概率的书籍当中,很少结合工程应用来说明概念和实际的对应关系,导致中间缺少一个可以让工程师充分理解的概念体系:
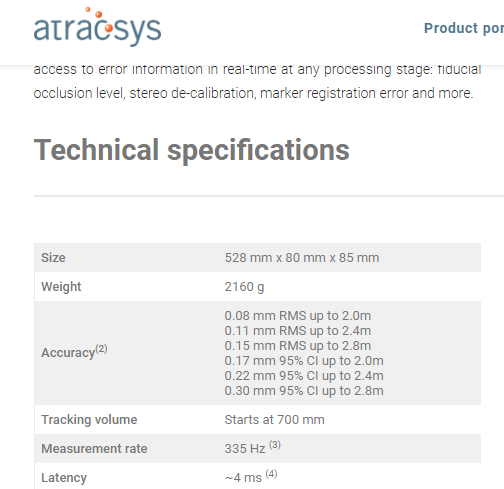
比如你作为某公司机器人系统研发工程师,在拿到如下的产品性能参数之后,需要开发一套可以稳定准确跟踪目标的机器人系统,这个系统可以输出空间内的特定目标的三维坐标和旋转信息,但是它的输出数据具有误差,那个RMS就代表了在不同的深度下(对于相机而言)你的系统使用到的数据的不确定性。例如在距离相机2.4m的标记点,测量数据和实际值之间最差会达到0.11mm,凭借直觉你肯定在想,假如真实值是
最基本的我认为是状态量或者测量量是随着时间变化的,是一个变量,而这个变量自带一个概率的分布,就是随机变量的分布函数
我们对随机变量的估计是根据测量数据而得到的,怎样把测量值考虑进去?不能绝对地相信测量值,因为传感器有误差,不能绝对地相信先验分布,因为很多时候不可能掌握,比如自动驾驶汽车在碎石路上行驶的过程中地面的摩擦系数变化很大,车轮容易打滑,汽车的纵向速度随时都有可能发生变化,所以需要根据车轮上的编码器和车辆的运动模型折中地做出估计。
连续随机变量
需要解决的问题: 1. 贝叶斯公式推导的是单独事件的概率,实际应用过程中需要的是对连续随机变量的概率密度函数进行后验估计,怎么做? 2. 前面的内容都是需要在已知全样本以及对应的概率情况下计算当前的后验概率分布,但是实际情况中,我们无法预先知道全样本的分布情况,也不可能重复多次做实验来得到全样本,因为首先一点是连续变量理论上没有办法做有限的实验来覆盖所有的情况。
上面的问题对应于贝叶斯统计的相关知识。
贝叶斯统计推断的基础是总体信息,样本信息和先验信息。三个概念是后面推导的定性指导,可以帮助我们对公式进行变形。
总体信息是总体的分布或者是总体所属分布族提供的信息。 我对总体信息的理解是包含了并不需要很细致的参数信息,例如只是知道了分布是正态分布,并不清楚期望和方差是多少,或者书中举的例子,我国确认国产轴承寿命分布是韦布尔分布花费了五年时间。
样本信息是抽取样本所得观测值提供的信息,属于本次实验得到的结果。它可以进一步让人了解总体分布的具体参数,例如总体均值,总体方差等等。有了样本,才有了统计学,才可以通过计算机具体地描述这个分布的特性,也就是参数化这个分布(或者穷举出来)
先验信息,是和前面的样本信息对应的,就是在做实验之前,需要首先了解这个问题在历史上或者经验情况,利用这种信息得到的分布叫做先验分布。 我的理解:例如历史经验,根据牛顿第二定律,力,速度,加速度,位移具有一定的约束关系,如果我们关心的随机变量是速度,但是我们知道加速度和受力的关系,那么,通过函数的映射,就可以得到速度的分布。-- 这里我的理解可能比较牵强,需要后面再次确认是否正确,因为这里可能是对随机变量的函数的分布的理解。
摘录书中的原话: > 贝叶斯学派的基本观点是:任一未知量
贝叶斯公式的概率密度函数形式: 原书中介绍得已经很详细了,这里不再重复,只是写出来我的理解。 1.
基本的概念清楚了之后,我们关心的是后验概率,因为贝叶斯的统计推断就是得到后验概率来更准确地描述随机变量的分布情况。
当测量值是
所以我们先写成概率分布函数,然后计算完概率分布函数之后对变量求导数,就得到了这个变量的概率密度函数。准确地说是条件概率分布函数:
然后根据贝叶斯后验概率计算公式,尝试写一下求和后面的部分:
但是上面的式子是不能这么写的,因为分母是0。
改写为极限的形式:
所以需要寻找一种恰当的表达方式来说明问题,根据连续变量的条件分布-- 3.5.1 条件分布 二 连续变量的条件分布:如果随机变量的概率密度函数是连续可导的,那么,取一个极限表达。 一般地,描述连续随机变量的概率分布写成贝叶斯公式如下:
看到局部区间的概率,可以使用概率密度函数进行替代:
求和和取极限之间没有关系,把取极限放入到求和公式内部并且利用积分中值定理得到,注意等式右边的积分范围是
上面的式子代入到求和公式当中,得到:
推导到这里,再利用积分的定义, 就可以得到连续随变量的后验概率分布公式:
在书里面概率密度函数写为
总结
贝叶斯滤波认为对随机变量的估计需要有一个先验的分布,也需要有采样得到的样本,这样综合起来把对随机变量的分布重新按照后验的方式进行估计,得到的分布结果是更接近于真实情况的。
参考
The Hilbert Space of Random Variables Electrical Engineering 126 (UC Berkeley)
An Elementary Introduction to Kalman Filtering