矩阵的奇异值分解

Besides having a rather simple geometric explanation, the singular value decomposition offers extremely effective techniques for putting linear algebraic ideas into practice.

SVD分解与四个子空间

任意的线性变换都可以进行奇异值分解(SVD: Singular Value Decomposition)。之前的一篇博客讲的特征值和特征向量都是针对方阵而言的.这里任意形状的矩阵都能够进行SVD变换。给定一个的矩阵，，这里需要特别说明，我们可以在这个矩阵的行空间和列空间内找到个线性无关的基，即使行、列空间的维度有不同。此处是核心：我们能够参考方阵，对它的特征值特征向量的推导过程得到启发，结合这里矩阵不一定是方阵（行、列维度不同的特点），能否在行子空间内找到一组相互正交的单位基向量，这组基向量通过的变换在列空间内“生产”出一组也是相互正交的向量，并且这组向量正好是列空间的一组基。

() 中，是行空间内的单位向量，且，是列空间内的单位向量（Orthonormal basis），且，是列空间内单位向量的伸缩系数。写成矩阵乘法的形式如下：

写成更简单的形式是：。

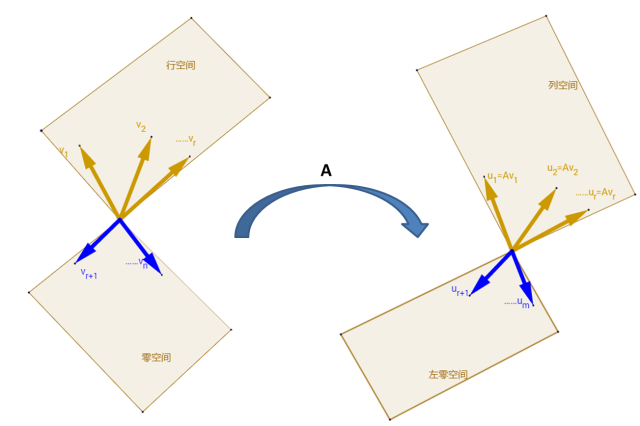
矩阵对行空间向量的变换 2025-06-13

费这么大的劲把矩阵的最本质的东西提取出来，一定是有目的的：

我们希望了解，任何一个矩阵，它在和两个空间内，具有什么样的结构：具体体现在行空间和列空间内的一组单位正交基：和，它们的数量和方向决定了这个矩阵对向量的变换能力。
我们希望给定任何一个向量：，能够不用按照矩阵和向量相乘的方法，用人更能够理解的方式把这个向量换坐标系，过程是：

向投影，得到在各个方向上的拉伸系数
因为经过变换之后，得到方向是，长度是，所以，经过变换之后，在方向上的拉伸长度是
写成矩阵形式：

所以主要工作量主要是第一步，求投影的拉伸系数。

矩阵对输入向量的变化，在一些方向上变换较大，在另一些方向变换较小，实际生产生活中，只是去关注变换较大的方向，忽略变换较小的方向：挑选那些较大们，对输入向量只针对这些方向做投影得到的拉伸系数就可以完成变换，节省计算资源，节省时间，达到的效果和全部计算没有显著区别。

奇异值分解的几何意义

接上面的矩阵定义，我们看一下空间的任意对象是如何变换的。

()中，是在行空间、零空间的坐标值，其中前个向量是行空间的分量，后面的是零空间的分量。并且，可以把这个对象想象成在内的单位球体。线性变换：

()少了后面的个分量，是因为。到这里，我们理解奇异值分解的几何意义就是：矩阵的奇异值分解，是在行空间内找到一组相互垂直的单位向量，这组向量经过矩阵的变换在列空间得到的向量也是相互垂直，观察()，旧坐标值和奇异值相乘的意义就是在新的基方向上，进行奇异值大小的拉伸操作。更加形象的理解就是，将单位球面变换为超椭球面，这个球面具有r$个半轴，每个半轴对应的奇异值是该半轴伸缩的系数。

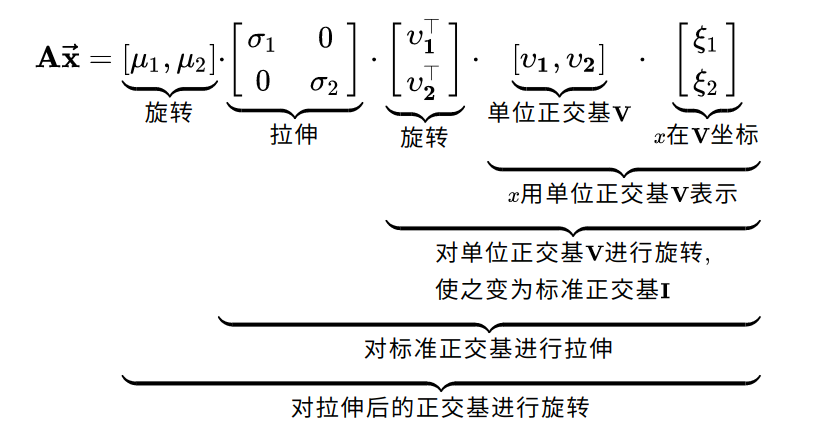
最近在知乎上又看到了硬核机器学习文章分享的回答，在他的回答中，两组正交基分别就是矩阵行空间、列空间的标准正交基。如果不好记忆的话，我们可以对比矩阵和向量的乘法，向量的维度和矩阵的行向量是一致的，所以向量是用来分解给定的向量的，这样我们就很容易得到酉矩阵的列向量是原矩阵列向量的一组标准正交基构成。

总结一下

步骤如下：

给出任意向量
矩阵对该向量的变换分解为如下
投影到，得到投影矢量为
使用旋转行基到单位标准正交基
使用奇异值拉伸的各个分量
使用旋转拉伸后的基向量，得到最终基，变换在该基下的分矢量就是

和特征值分解的关系

刚才只讨论了矩阵行空间和列空间的向量，那么，剩下的零空间和左零空间的向量难道就放弃了么？并不是这样的，出于考虑问题的完备性，我们写出如下的表达式

SVD更广泛的意义是将（行空间+零空间）内的一组标准正交基和（列空间+左零空间）的标准正交基拉进来，形式上完备了，具体矩阵所具有的特性取决于中间对角矩阵中非零奇异值的个数，理想的情况是，当矩阵是一个方阵时，并且具有个特征向量，那么行空间和列空间的维度是一样的，通过SVD分解矩阵得到的中，各列就是该矩阵的特征向量。从这点上，我们可以得到，方阵的特征向量特征值是矩阵SVD分解的特殊情况。