投影矩阵和最小二乘
投影矩阵
之前的一篇博客讲到了矩阵的四个子空间:行空间,列空间,零空间和左零空间。每一个空间唯一性地由这个矩阵决定,因为这个矩阵的列可能线性无关,可能线性相关,如果线性相关,能够在其中找到多少个线性无关的向量。所以,不同的矩阵所形成的对应的四个子空间情况各不相同。我们为了能够理解给定的矩阵四个空间分布情况,就引入了投影矩阵的概念,用来分析在空间中任意向量到这个矩阵的“距离”。下面我们具体看一下:
首先回顾一下矩阵的列空间
给定任意一个与
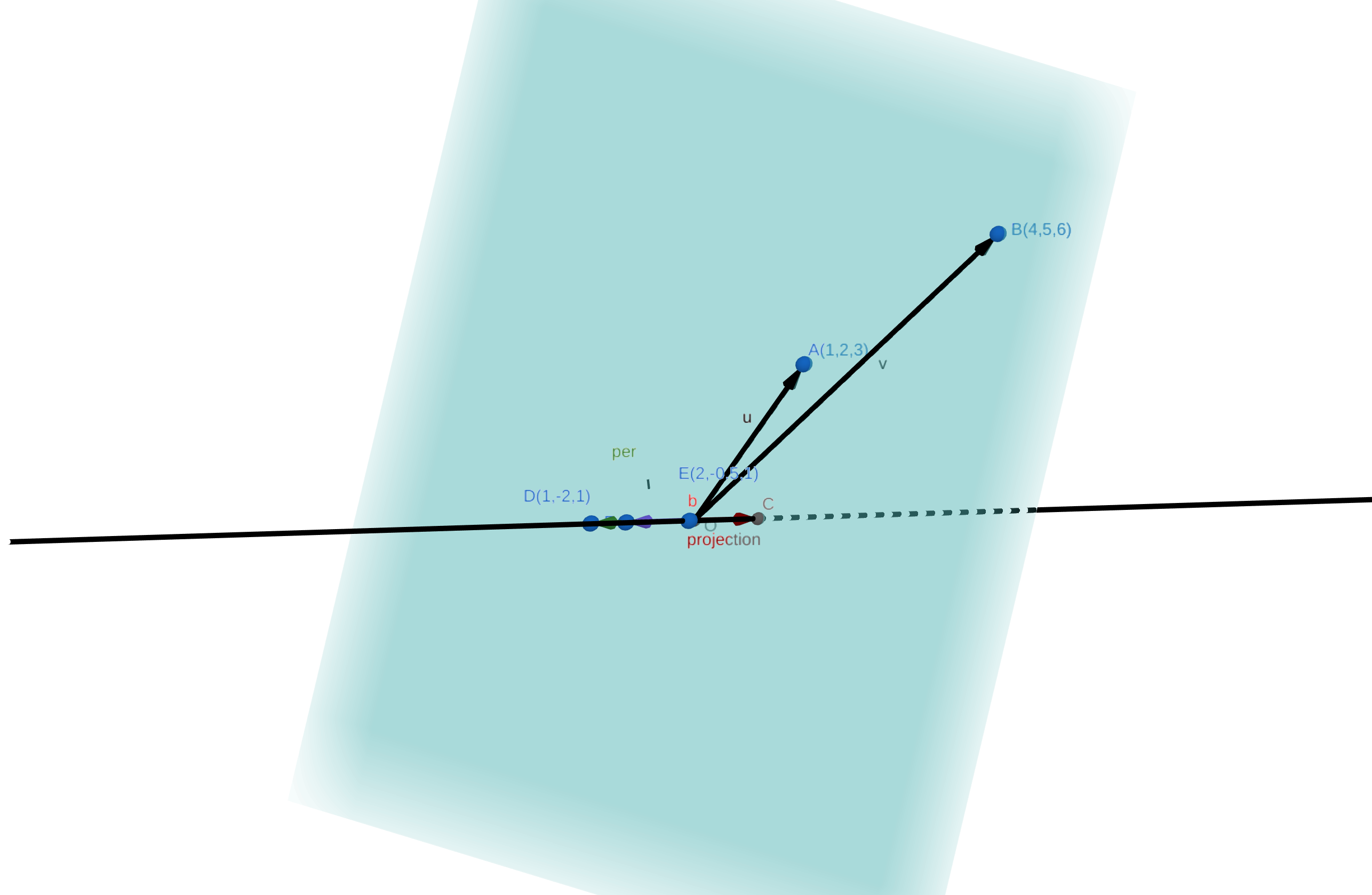
两个列向量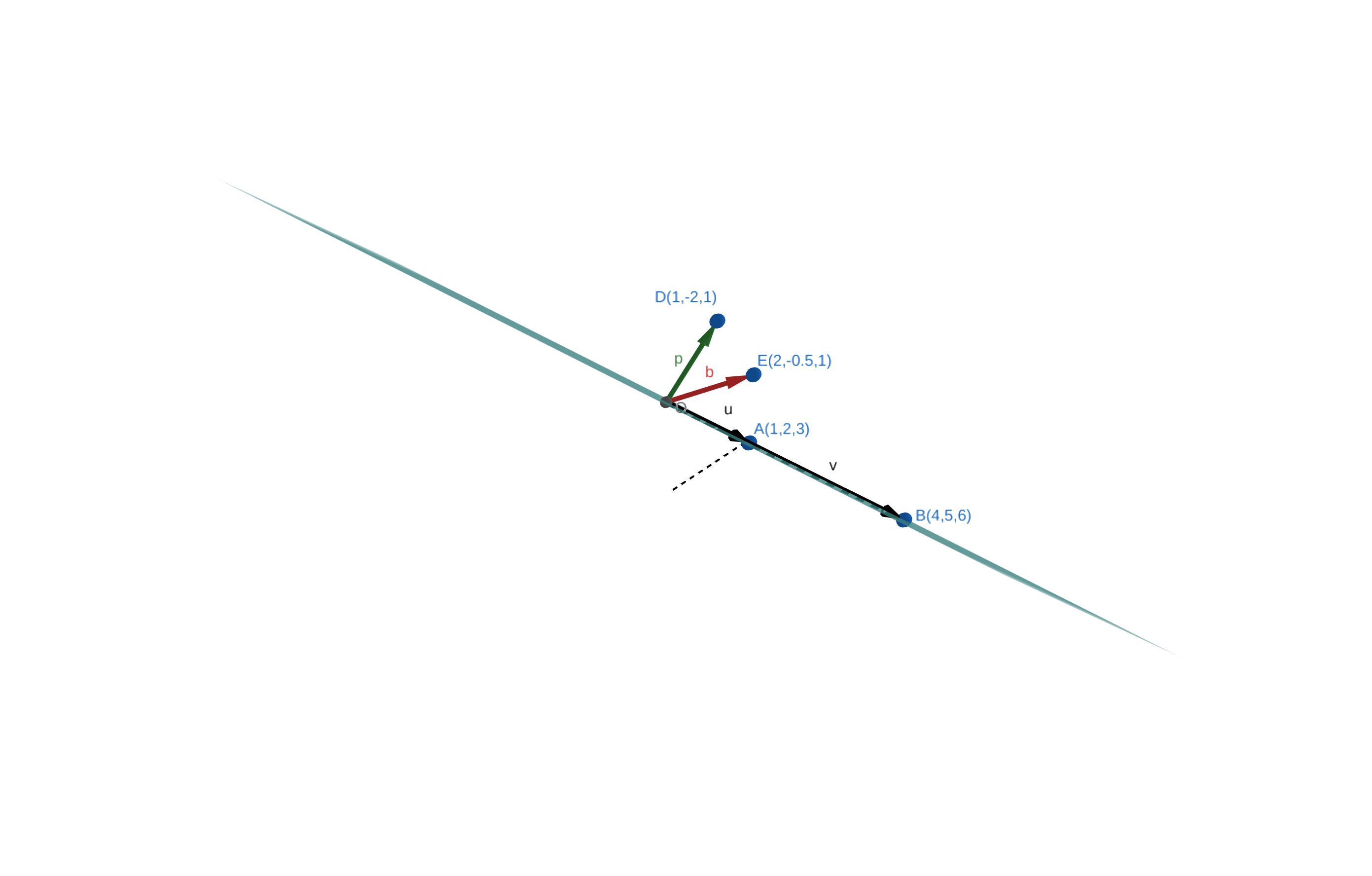
 那么,投影矩阵对该任意向量的作用就是将这个向量对列空间投影,得到
那么,投影矩阵对该任意向量的作用就是将这个向量对列空间投影,得到
投影矩阵的性质
- 幂等性(idempotent):
最小二乘
问题描述
已知空间当中的一些点,如何找到一条直线,能够尽可能地离所有点最近?
问题梳理
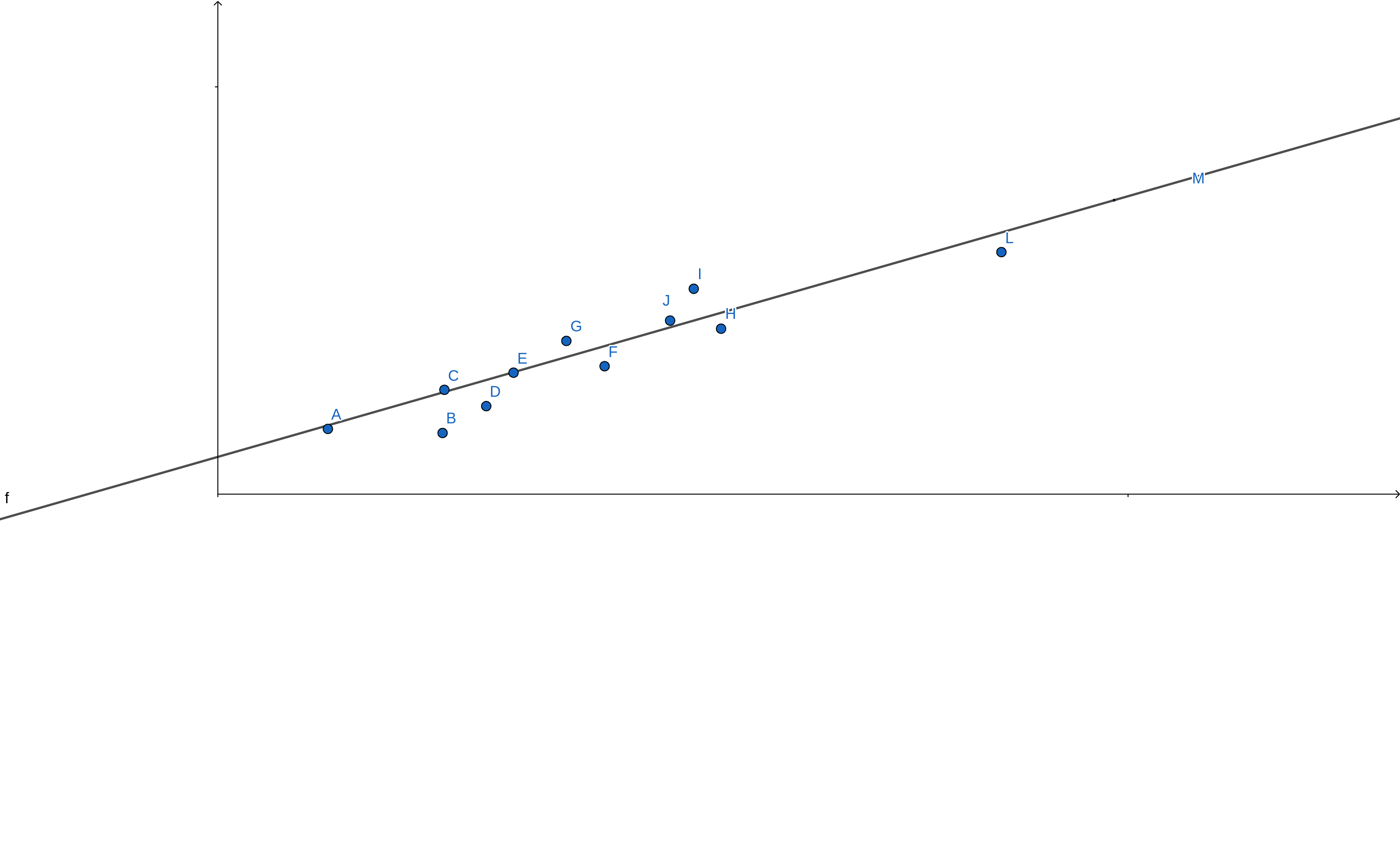 假设二维空间有
假设二维空间有
为了最小化这个式子,根据式子的特点,我们可以将问题转化成为通过寻找向量的模长的最小值解决。这个向量是:
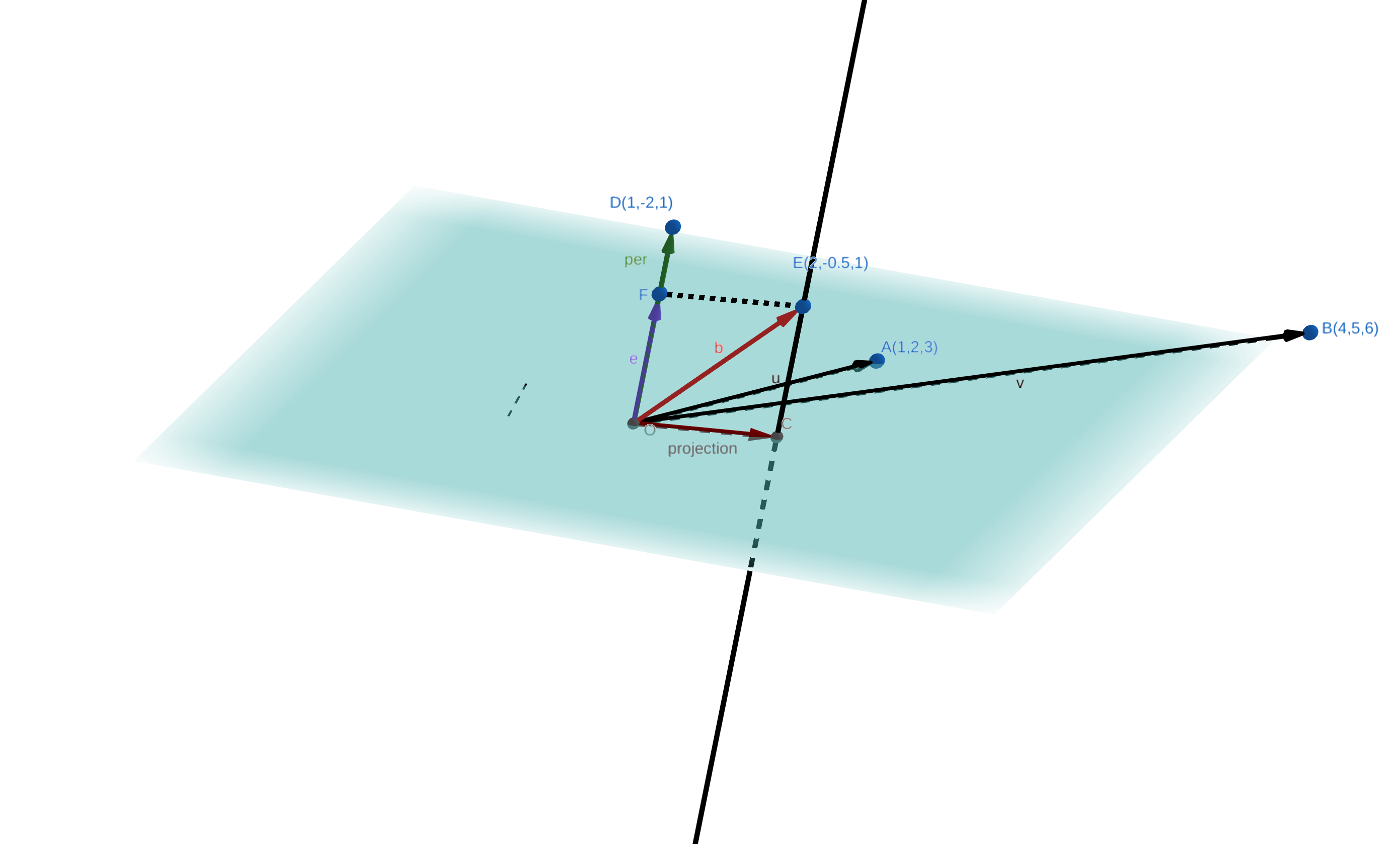
投影已知向量
最小化该向量的长度,就是尽可能地在矩阵
投影在列空间上面的分量
解方程组
得到的解就是最小二乘的解。其实也是投影向量在列空间的坐标值。
高维度下的推广
上面是以维度为2举例子,如果扩展到高维度(
补充
在上面提到的最小化
需要继续思考的内容
Dot Product 这个视频讲解了向量点积的深层理解,说到了向量点积也可以理解为其中一个向量充当只有一行的变换矩阵,这个矩阵是用来投影的,并且还分析了矩阵里面的每一个元素其实就是空间基向量向这个向量的投影,还是这个向量向基向量的投影!因为投影具有对称的性质,这个视频很不错,值得一看。